CF10B.Cinema Cashier

All cinema halls in Berland are rectangles with $K$ rows of $K$ seats each, and $K$ is an odd number. Rows and seats are numbered from $1$ to $K$ . For safety reasons people, who come to the box office to buy tickets, are not allowed to choose seats themselves. Formerly the choice was made by a cashier, but now this is the responsibility of a special seating program. It was found out that the large majority of Berland's inhabitants go to the cinema in order to watch a movie, that's why they want to sit as close to the hall center as possible. Moreover, a company of $M$ people, who come to watch a movie, want necessarily to occupy $M$ successive seats in one row. Let's formulate the algorithm, according to which the program chooses seats and sells tickets. As the request for $M$ seats comes, the program should determine the row number $x$ and the segment $[y_{l},y_{r}]$ of the seats numbers in this row, where $y_{r}-y_{l}+1=M$ . From all such possible variants as a final result the program should choose the one with the minimum function value of total seats remoteness from the center. Say, 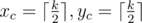— the row and the seat numbers of the most "central" seat. Then the function value of seats remoteness from the hall center is 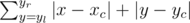. If the amount of minimum function values is more than one, the program should choose the one that is closer to the screen (i.e. the row number $x$ is lower). If the variants are still multiple, it should choose the one with the minimum $y_{l}$ . If you did not get yet, your task is to simulate the work of this program.
贝兰德的所有电影院都是长方形，有 K 排，每排有 K 个座位， K 是奇数。每排和每个座位的编号从 1 到 K 。出于安全考虑，到售票处购票的人不能自己选择座位。以前是由收银员进行选择，现在则由专门的座位程序负责。据调查，大部分贝兰德居民去电影院都是为了看电影，因此他们希望坐在尽可能靠近大厅中心的位置。此外， M 个前来观看电影的观众必须在一排中占据 M 个连续座位。让我们计算一下程序选择座位和出售门票的算法。当 M 个座位的请求出现时，程序应确定行号 x 和该行座位号的段 [yl, yr] ，其中 yr - yl + 1 = M 个座位。作为最终结果，程序应从所有可能的变体中选择座位总数与中心距离函数值最小的变体。例如

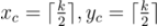
，--最 "中心 "座位的行号和座位号。那么，座位与大厅中心距离的函数值为

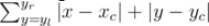
。如果最小函数值的数量多于一个，程序应选择离屏幕较近的一个(即行号 x 较低)。如果仍有多个变量，则应选择最小值为 yl 的变量。如果你还没有得到答案，那么你的任务就是模拟这个程序的工作。

The first line contains two integers $N$ and $K$ ( $1<=N<=1000,1<=K<=99$ ) — the amount of requests and the hall size respectively. The second line contains $N$ space-separated integers $M_{i}$ from the range $[1,K]$ — requests to the program.
输入
第一行包含两个整数 N 和 K ( 1 ≤ N ≤ 1000, 1 ≤ K ≤ 99 )--分别是请求数量和大厅大小。第二行包含 N 个空格分隔的整数 Mi ，范围为 [1, K] --向程序提出的请求。

Output $N$ lines. In the $i$ -th line output «-1» (without quotes), if it is impossible to find $M_{i}$ successive seats in one row, otherwise output three numbers $x,y_{l},y_{r}$ . Separate the numbers with a space.
输出
输出 N 行。如果无法在一行中找到 Mi 个连续座位，则在第 i 行输出"-1"(不带引号)，否则输出三个数字 x, yl, yr 。数字之间用空格隔开。