A35244.画图

时间限制:1S
空间限制:512mb
样例文件:Draw

小 N 有一棵 $n$ 个结点的无根树，现在他想将原树通过一种新的方式画下来。

他的画图操作可以看成是对一个树上连通块生成一棵有根树：

1. 选择连通块的一个结点 $r$ 作为有根树的根，然后将结点 $r$ 删除，令有 $k$ 个结点，$p_1,p_2,\cdots,p_k$ 与结点 $r$ 有边，得到包含结点 $p_i$ 的第 $i$ 个连通块；
2. 对第 $i\in[1,k]\cap \mathbb{Z}$ 个连通块进行画图操作，并将结点 $r$ 与第 $i$ 个连通块操作后的有根树根结点连边。这样就得到了一个新的有根树。

由此，小 N 对整棵树按照上述过程得到一个 $n$ 个结点的有根树。现在，小 N 想知道有多少种本质不同的有根树，对 $10^9+7$ 取模。

两棵有根树本质不同，当且仅当根不同，或者存在一个点的父亲不同。

第一行一个正整数 $n$ 表示树的点数。

接下来 $n - 1$ 行，第 $i$ 行包含两个整数 $u_i, v_i$，表示树上编号为 $i$ 的边连接结点 $u_i$ 和 $v_i$。

一行一个整数，表示答案对 $10^9+7$ 取模后的值。

样例解释 1

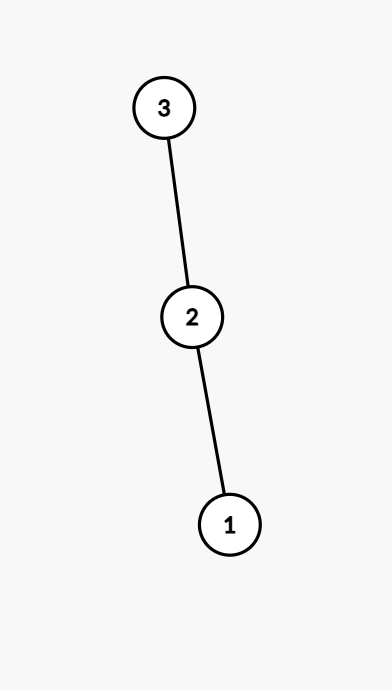
下面 $5$ 张图分别对应 $5$ 种本质不同的有根树：

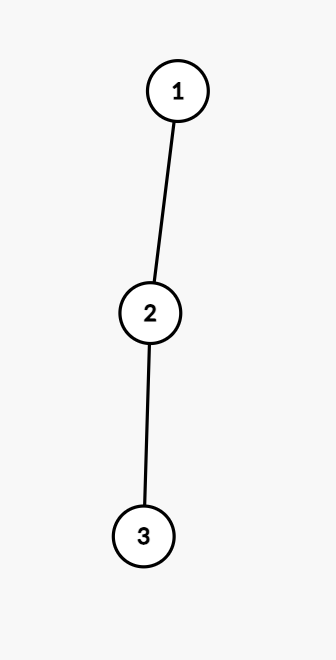
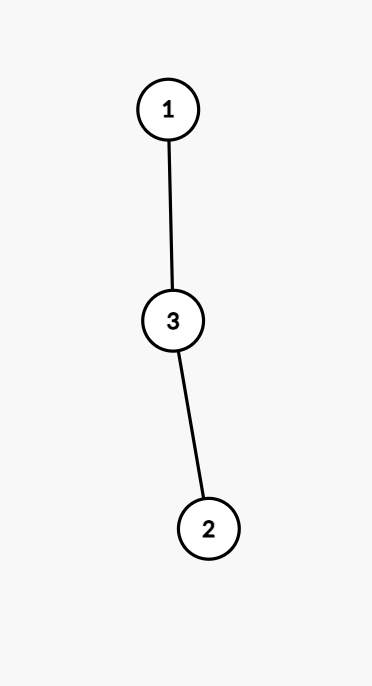
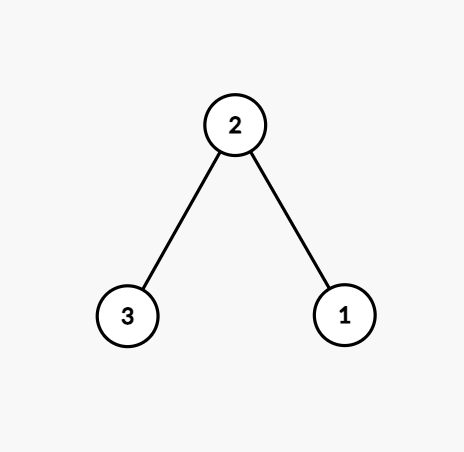
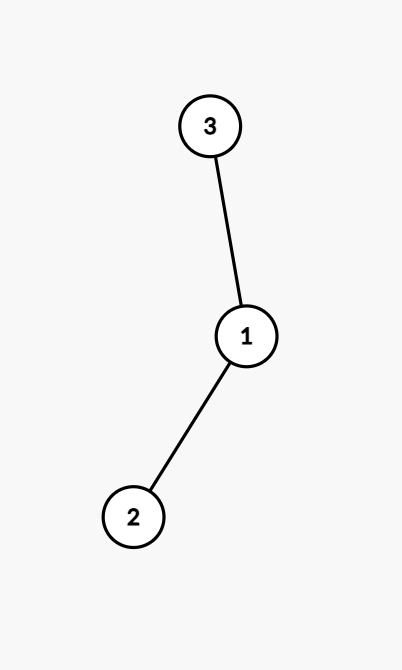
数据范围

对于所有的测试数据，保证：

• $1 \leq n \leq 5000$；
• 对于任意的 $i(1 \leq i \leq n - 1)$，都有 $1 \leq u_i, v_i \leq n$，且构成一颗合法的树。

测试点编号	$n\le$	特殊性质
$1\sim 3$	$10$	无
$4\sim 6$	$20$	无
$7,8$	$30$	C
$9,10$	$30$	无
$11,12$	$50$	C
$13,14$	$50$	无
$15,16$	$100$	C
$17,18$	$100$	无
$19,20$	$300$	C
$21$	$300$	无
$22$	$5000$	A
$23$	$5000$	B
$24$	$5000$	C
$25$	$5000$	无

• 特殊性质 A：保证 $\forall i\in [1, n-1]\cap \mathbb{Z}$，满足 $i$ 和 $i+1$ 有边；
• 特殊性质 B：保证 $\forall i\in [2, n]\cap \mathbb{Z}$，满足 $1$ 和 $i$ 有边；
• 特殊性质 C：保证树的生成方式形如，对于结点 $i\in [2,n]$，在 $[1,i-1]$ 内等概率随机一个点 $p$，将 $i,p$ 连一条边。