A33356.特殊的染料

给定 $N$ 个容量为 $N$ 的染料桶 $1, 2, \cdots, N$ 从左到右排成一行。其中每个桶中都有装有 $A_i$ 个单位的「颜色」为 $A_i$ 的染料，每个桶中的染料量 互不相同。

这种染料有一种特殊性质：将「颜色」为 $X$ 的染料倒在「颜色」为 $Y$ 的染料的上方，则两种染料 不会混合，染料 $X$ 会完整地浮在染料 $Y$ 的上方。

你可以通过执行以下操作，来使所有桶中的染料量从左到右递增。

1. 选择一个 $i\ (1 \le i \lt N)$，将桶 $i$ 中的染料和桶 $i + 1$ 中的染料进行「倒换」。
2. 每次「倒换」需要选择一个桶 $j\ (j \ne i, j \ne i + 1)$，若当前桶 $j$ 中的染料的颜色为 $k$ 则消耗 $B_k$ 枚金币，将桶 $j$ 当作交换中介，来完成此次「倒换」；
3. 具体地：将桶 $i$ 或 $i + 1$ 中的染料倒入 $j$ 中。此处以 $i$ 为例，先将桶 $i$ 中的染料倒入 $j$ 中，但不能超出桶的容量，令当前两桶中的染料量分别为 $A_i$ 和 $A_j$，那么要求 $A_i + A_j \le N$；此时桶 $i$ 空置，将桶 $i + 1$ 中的染料倒入 $i$ 中，此时桶 $i + 1$ 空置；再将桶 $j$ 中的上方的染料倒入桶 $i + 1$ 中，完成「倒换」操作；反之先将桶 $i + 1$ 中的染料倒入 $j$ 中亦可，但需要满足 $A_{i + 1} + A_j \le N$。

请你计算完成排序任务最少需要消耗多少枚金币。

$\large{数据范围}$

• $3 \le N \le 100$
• $1 \le A_i \le N$
• $1 \le B_i \le 100$
• 所有输入数据均为整数。

对于每个测试文件输入格式如下：

$\tt{N}$
$\tt{A_1\ A_2\ A_3\ \cdots\ A_N}$
$\tt{B_1\ B_2\ B_3\ \cdots\ B_N}$

对于每个测试文件在单独的一行中输出答案。

$\bf{样例\ 1：}$

按照以下步骤执行操作，使用 $2$ 枚金币将装有「蓝色」颜料的桶 $1$ 当作「中介」，倒换桶 $2$ 和 桶 $3$ 中的染料，使得所有桶中的染料量从左到右递增。

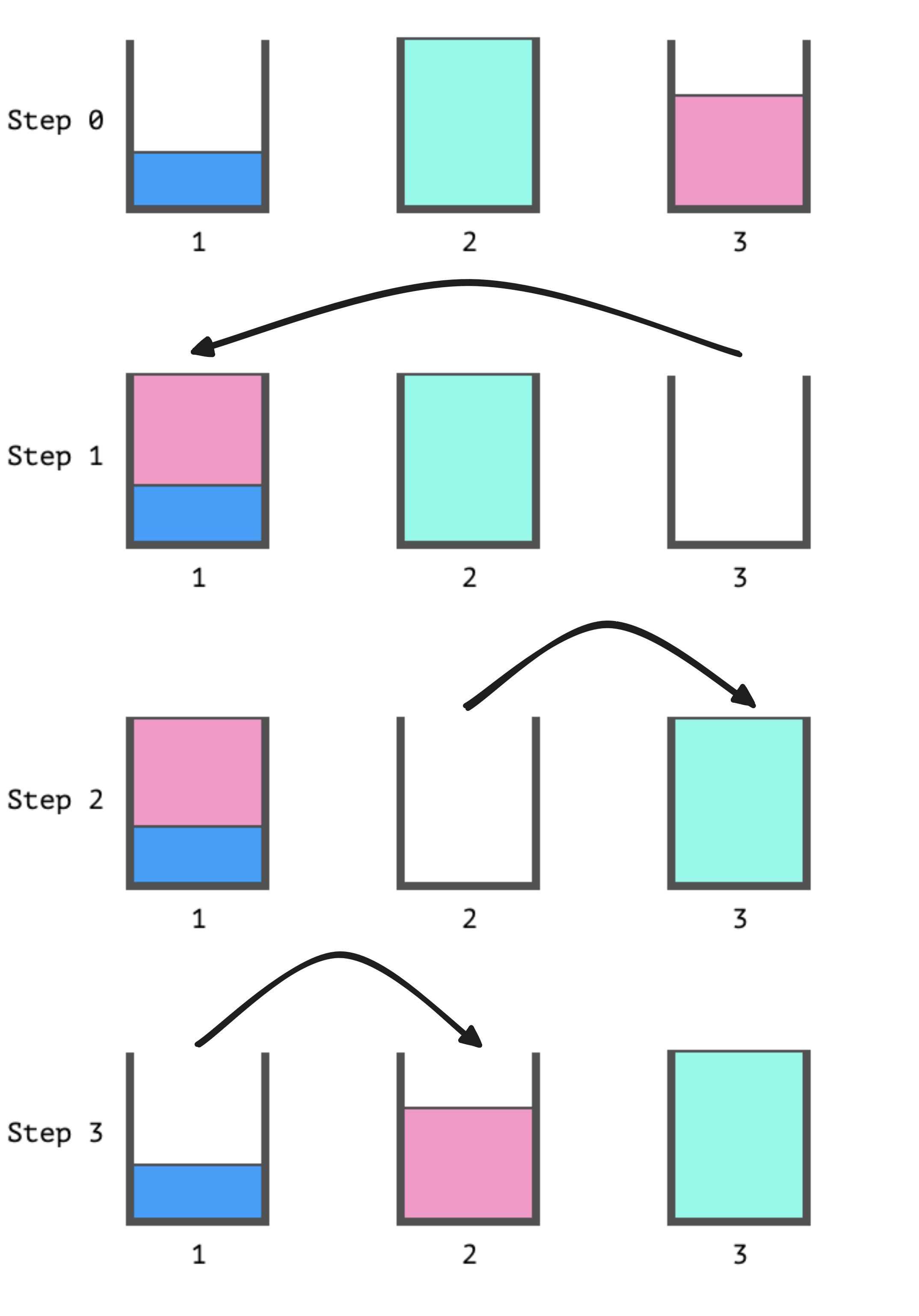
$\bf{样例\ 2：}$

请注意，「倒换」操作花费的金币，仅与当作「中介」的桶中染料的颜色有关，与桶的编号无关。

1. 对于 $2$ 号桶和 $3$ 号桶中的染料，花费 $9$ 枚金币把装有颜色 $1$ 的染料桶当作「中介」，进行倒换，顺序变为 $4, 2, 5, 1, 3$。
2. 对于 $3$ 号桶和 $4$ 号桶中的染料，花费 $7$ 枚金币把装有颜色 $2$ 的染料桶当作「中介」，进行倒换，顺序变为 $4, 2, 1, 5, 3$。
3. 对于 $4$ 号桶和 $5$ 号桶中的染料，花费 $7$ 枚金币把装有颜色 $2$ 的染料桶当作「中介」，进行倒换，顺序变为 $4, 2, 1, 3, 5$。
4. 对于 $1$ 号桶和 $2$ 号桶中的染料，花费 $9$ 枚金币把装有颜色 $1$ 的染料桶当作「中介」，进行倒换，顺序变为 $2, 4, 1, 3, 5$。
5. 对于 $2$ 号桶和 $3$ 号桶中的染料，花费 $7$ 枚金币把装有颜色 $2$ 的染料桶当作「中介」，进行倒换，顺序变为 $2, 1, 4, 3, 5$。
6. 对于 $3$ 号桶和 $4$ 号桶中的染料，花费 $7$ 枚金币把装有颜色 $2$ 的染料桶当作「中介」，进行倒换，顺序变为 $2, 1, 3, 4, 5$。
7. 对于 $1$ 号桶和 $2$ 号桶中的染料，花费 $8$ 枚金币把装有颜色 $4$ 的染料桶当作「中介」，进行倒换，顺序变为 $1, 2, 3, 4, 5$。

共计花费 $9 + 7 + 7 + 9 + 7 + 7 + 8 = 54$ 枚金币，使得所有桶中的染料量从左到右递增。