CF1906G.Grid Game 2

You are playing "Grid Game 2" with your friend. There is a grid with $10^9$ rows (numbered from $1$ to $10^9$) and $10^9$ columns (numbered from $1$ to $10^9$). The cell at row $r$ and column $c$ is denoted as $(r, c)$.

Each cell can have a colour of either black or white. Initially, there are exactly $N$ black cells (numbered from $1$ to $N$). Black cell $i$ is located at $(R_i, C_i)$. The rest of the cells are white.

You and your friend will alternately take turn playing on this grid, and you are playing in the first turn. In one turn, a player will choose a black cell $(r, c)$, then toggle cells $(r - x, c - y)$ for all $0 \leq x, y \lt \min(r, c)$. If a cell is toggled, then the cell becomes black if it was a white cell, and the cell becomes white if it was a black cell.

For example, the following illustration shows how the grid changes after a player chooses a black cell $(5, 4)$ in their turn.

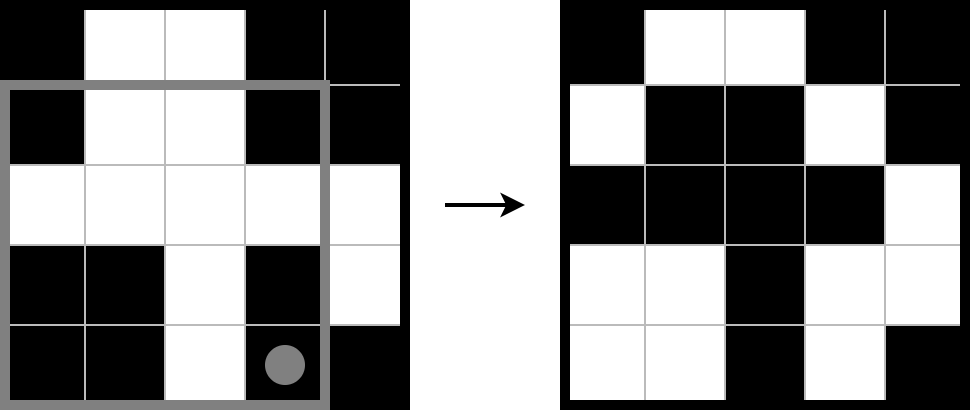A player who is unable to play on their turn, i.e. no remaining black cells, loses the game, and the opposing player wins the game. If you and your friend are playing optimally, determine who will win the game.

你正在和朋友一起玩“网格游戏2”。有一个 $10^9$ 行（行号从 $1$ 到 $10^9$）和 $10^9$ 列（列号从 $1$ 到 $10^9$）的网格。第 $r$ 行第 $c$ 列的格子记为 $(r, c)$。

每个格子的颜色为黑色或白色之一。初始时，恰好有 $N$ 个黑格（编号为 $1$ 至 $N$），其中第 $i$ 个黑格位于 $(R_i, C_i)$；其余所有格子均为白色。

你和朋友将轮流在该网格上进行游戏，你先行。在一轮中，玩家需选择一个黑格 $(r, c)$，然后对所有满足 $0 \leq x, y < \min(r, c)$ 的格子 $(r - x, c - y)$ 进行翻转：若某格原为白色，则变为黑色；若原为黑色，则变为白色。

例如，下图展示了当一名玩家在自己的回合中选择黑格 $(5, 4)$ 后，网格的变化情况：

若某玩家在其回合开始时已无黑格可选（即不存在任何黑格），则该玩家输掉游戏，对手获胜。若你和朋友均以最优策略进行游戏，请判断谁将获胜。

The first line consists of an integer $N$ ($1 \le N \le 200\,000$).

Each of the next $N$ lines consists of two integers $R_i$ $C_i$ ($1 \leq R_i, C_i \leq 10^9)$. For $1 \leq i \lt j \leq N$, $(R_i, C_i) \neq (R_j, C_j)$.

第一行包含一个整数 $N$（$1 \le N \le 200\,000$）。

接下来的 $N$ 行，每行包含两个整数 $R_i$ 和 $C_i$（$1 \leq R_i, C_i \leq 10^9$）。对于所有满足 $1 \leq i \lt j \leq N$ 的 $i,j$，均有 $(R_i, C_i) \neq (R_j, C_j)$。

Output FIRST if you will win the game, or SECOND otherwise.

如果你会赢得游戏，输出 FIRST；否则输出 SECOND。

Explanation for the sample input/output #1

You can start your move by choosing $(2, 4)$, whose effect was demonstrated in the following illustration.

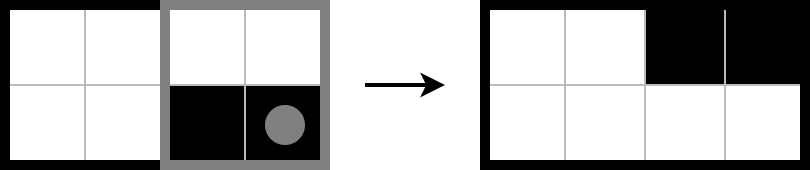The remaining black cells are $(1, 3)$ and $(1, 4)$, each of which will only toggle itself when chosen. Whichever your friend chooses on the next move, the you can choose the remaining black cell.

Explanation for the sample input/output #2

You have only one cell to choose, and will toggle cells $(1, 1)$, $(1, 2)$, $(2, 1)$, and $(2, 2)$. Your friend and you will alternately choose the remaining black cells with your friend choosing the last black cell.

样例输入/输出 #1 的说明

你可以选择起始操作位置 $(2, 4)$，其效果如下图所示。

剩余的黑色格子为 $(1, 3)$ 和 $(1, 4)$，当分别选择这两个格子时，仅会翻转其自身。无论你的朋友在下一步选择哪一个，你都可以在随后一步选择剩下的那个黑色格子。

样例输入/输出 #2 的说明

你唯一可选的格子将翻转 $(1, 1)$、$(1, 2)$、$(2, 1)$ 和 $(2, 2)$ 这四个格子。之后，你和你的朋友将轮流选择剩余的黑色格子，且由你的朋友选择最后一个黑色格子。