CF1916F.Group Division

In the $31$st lyceum, there were two groups of olympiad participants: computer science and mathematics. The number of computer scientists was $n_1$, and the number of mathematicians was $n_2$. It is not known for certain who belonged to which group, but it is known that there were friendly connections between some pairs of people (these connections could exist between a pair of people from the same group or from different groups).

The connections were so strong that even if one person is removed along with all their friendly connections, any pair of people still remains acquainted either directly or through mutual friends.

$^{\dagger}$ More formally, two people $(x, y)$ are acquainted in the following case: there are people $a_1, a_2, \ldots,a_n$ ($1 \le a_i \le n_1 + n_2$) such that the following conditions are simultaneously met:

$\bullet$ Person $x$ is directly acquainted with $a_1$.

$\bullet$ Person $a_n$ is directly acquainted with $y$.

$\bullet$ Person $a_i$ is directly acquainted with $a_{i + 1}$ for any ($1 \le i \le n - 1$).

The teachers were dissatisfied with the fact that computer scientists were friends with mathematicians and vice versa, so they decided to divide the students into two groups in such a way that the following two conditions are met:

$\bullet$ There were $n_1$ people in the computer science group, and $n_2$ people in the mathematics group.

$\bullet$ Any pair of computer scientists should be acquainted (acquaintance involving mutual friends, who must be from the same group as the people in the pair, is allowed), the same should be true for mathematicians.

Help them solve this problem and find out who belongs to which group.

在第31中学，有两组参加奥赛的学生：计算机科学组和数学组。计算机科学组的人数为 $n_1$，数学组的人数为 $n_2$。目前尚不能确定每个人具体属于哪一组，但已知某些人之间存在友谊关系（这些友谊关系可能存在于同一组内的两人之间，也可能存在于不同组的两人之间）。

这些友谊关系极为牢固：即使移除某一个人及其所有友谊连接，任意两人之间仍能通过直接相识或经由共同朋友间接相识而保持“相识”关系。

$^{\dagger}$ 更严格地定义，“相识”关系如下：对两个人 $(x, y)$，若存在一系列人 $a_1, a_2, \ldots, a_n$（其中 $1 \le a_i \le n_1 + n_2$），使得以下条件同时成立，则称 $x$ 与 $y$ 相识：

$\bullet$ $x$ 与 $a_1$ 直接相识；
$\bullet$ $a_n$ 与 $y$ 直接相识；
$\bullet$ 对任意 $1 \le i \le n - 1$，$a_i$ 与 $a_{i + 1}$ 直接相识。

教师们对计算机科学组学生与数学组学生之间互为朋友的现象感到不满，因此决定将全体学生重新划分为两个组，满足以下两个条件：

$\bullet$ 计算机科学组恰好有 $n_1$ 人，数学组恰好有 $n_2$ 人；
$\bullet$ 任意两名计算机科学组学生之间必须相识（允许通过共同朋友间接相识，但这些共同朋友也必须同属计算机科学组）；同理，任意两名数学组学生之间也必须相识（中间共同朋友也必须同属数学组）。

请帮助他们解决该问题，确定每个人应归属的组别。

Each test consists of several test cases. The first line contains a single integer $t$ ($1 \le t \le 1000$) — the number of test cases. Then follows the description of the test cases.

The first line of each test case contains three integers $n_1$, $n_2$, and $m$ ($1 \le n_1, n_2 \le 2000$, $1 \le m \le 5000$). $n_1$, $n_2$ are the sizes of the two groups described in the problem, and $m$ is the number of friendly connections initially.

The following $m$ lines describe the friendly connections: in the $i$-th ($1 \le i \le m$) line, a pair of numbers $(a, b)$ is given, which means that the person with number $a$ is friends with the person with number $b$ (and vice versa).

It is guaranteed that for each test case, all friendly connections are distinct.

It is guaranteed that the sum of $n_1 + n_2$ for all test cases does not exceed $2000$, and the sum of $m$ for all test cases does not exceed $5000$.

It is also guaranteed that for each test case, a solution exists.

If there are several answers, print any of them.

每个测试包含若干个测试用例。第一行包含一个整数 $t$（$1 \le t \le 1000$），表示测试用例的数量。随后是各测试用例的描述。

每个测试用例的第一行包含三个整数 $n_1$、$n_2$ 和 $m$（$1 \le n_1, n_2 \le 2000$，$1 \le m \le 5000$）。其中 $n_1$、$n_2$ 分别为题目中所述两个组的大小，$m$ 为初始友好关系的数量。

接下来的 $m$ 行描述这些友好关系：第 $i$ 行（$1 \le i \le m$）给出一对数字 $(a, b)$，表示编号为 $a$ 的人与编号为 $b$ 的人互为朋友（关系是双向的）。

保证每个测试用例中所有友好关系互不相同。

保证所有测试用例的 $n_1 + n_2$ 之和不超过 $2000$，且所有测试用例的 $m$ 之和不超过 $5000$。

同时保证每个测试用例均有解。

若存在多个答案，输出任意一个即可。

For each test case, output two lines.

In the first line, output $n_1$ distinct numbers $a_i$ ($1 \le a_i \le n_1 + n_2$) — the people belonging to the first group.

In the second line, output $n_2$ distinct numbers $b_i$ ($1 \le b_i \le n_1 + n_2$) — the people belonging to the second group.

All numbers must be distinct.

If there are several possible answers, print any one.

对于每个测试用例，输出两行。

第一行输出 $n_1$ 个互不相同的数 $a_i$（$1 \le a_i \le n_1 + n_2$）——属于第一组的人。

第二行输出 $n_2$ 个互不相同的数 $b_i$（$1 \le b_i \le n_1 + n_2$）——属于第二组的人。

所有数字必须互不相同。

如果存在多种可能的答案，输出任意一个即可。

Consider the third test case. The division into groups looks as follows:

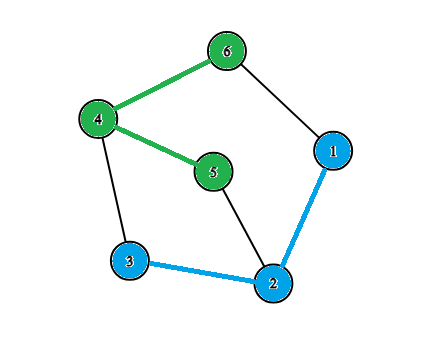The students selected as computer scientists are colored in green, and those selected as mathematicians are colored in blue.

Consider all pairs of computer scientists and how they are acquainted:

Pairs $(4, 5), (4, 6)$ are directly acquainted.

Pair $(5, 6)$ is acquainted through the computer scientist with number $4$.

Consider all pairs of mathematicians and how they are acquainted:

Pairs $(1, 2), (2, 3)$ are directly acquainted.

Pair $(1, 3)$ is acquainted through the mathematician with number $2$.

We conclude that any pair of people belonging to the same group is acquainted with each other, thus the division into two groups is correct.

考虑第三个测试用例。分组情况如下所示：

被选为计算机科学家的学生以绿色标出，被选为数学家的学生以蓝色标出。

考虑所有计算机科学家之间的配对及其相识关系：

配对 $(4, 5)$、$(4, 6)$ 是直接相识的。

配对 $(5, 6)$ 通过编号为 $4$ 的计算机科学家而相识。

考虑所有数学家之间的配对及其相识关系：

配对 $(1, 2)$、$(2, 3)$ 是直接相识的。

配对 $(1, 3)$ 通过编号为 $2$ 的数学家而相识。

我们得出结论：同一组内的任意两人均彼此相识，因此划分为两个组是正确的。