CF1919H.Tree Diameter

There is a hidden tree with $n$ vertices. The $n-1$ edges of the tree are numbered from $1$ to $n-1$. You can ask the following queries of two types:

1. Give the grader an array $a$ with $n - 1$ positive integers. For each edge from $1$ to $n - 1$, the weight of edge $i$ is set to $a_i$. Then, the grader will return the length of the diameter$^\dagger$.
2. Give the grader two indices $1 \le a, b \le n - 1$. The grader will return the number of edges between edges $a$ and $b$. In other words, if edge $a$ connects $u_a$ and $v_a$ while edge $b$ connects $u_b$ and $v_b$, the grader will return $\min(\text{dist}(u_a, u_b), \text{dist}(v_a, u_b), \text{dist}(u_a, v_b), \text{dist}(v_a, v_b))$, where $\text{dist}(u, v)$ represents the number of edges on the path between vertices $u$ and $v$.

Find any tree isomorphic$^\ddagger$ to the hidden tree after at most $n$ queries of type 1 and $n$ queries of type 2 in any order.

$^\dagger$ The distance between two vertices is the sum of the weights on the unique simple path that connects them. The diameter is the largest of all those distances.

$^\ddagger$ Two trees, consisting of $n$ vertices each, are called isomorphic if there exists a permutation $p$ containing integers from $1$ to $n$ such that edge ($u$, $v$) is present in the first tree if and only if the edge ($p_u$, $p_v$) is present in the second tree.

存在一棵隐藏的、包含 $n$ 个顶点的树。该树的 $n-1$ 条边被编号为 $1$ 到 $n-1$。你可以提出以下两类查询：

1. 向评测程序提供一个长度为 $n - 1$ 的正整数数组 $a$。对于每条从 $1$ 到 $n - 1$ 的边，将边 $i$ 的权重设为 $a_i$。随后，评测程序将返回该加权树的直径$^\dagger$ 的长度。
2. 向评测程序提供两个下标 $1 \le a, b \le n - 1$。评测程序将返回边 $a$ 与边 $b$ 之间的边数。换言之，若边 $a$ 连接顶点 $u_a$ 和 $v_a$，边 $b$ 连接顶点 $u_b$ 和 $v_b$，则评测程序将返回

   $$\min(\text{dist}(u_a, u_b),\ \text{dist}(v_a, u_b),\ \text{dist}(u_a, v_b),\ \text{dist}(v_a, v_b)),$$

   其中 $\text{dist}(u, v)$ 表示顶点 $u$ 与 $v$ 之间路径上的边数。

在至多进行 $n$ 次第 1 类查询和 $n$ 次第 2 类查询（顺序任意）的前提下，找出任意一棵与隐藏树同构$^\ddagger$ 的树。

$^\dagger$ 两顶点间的距离定义为连接它们的唯一简单路径上所有边的权重之和；直径即为所有顶点对间距离的最大值。

$^\ddagger$ 若两棵各有 $n$ 个顶点的树满足：存在一个由 $1$ 到 $n$ 的整数构成的排列 $p$，使得第一棵树中存在边 $(u, v)$ 当且仅当第二棵树中存在边 $(p_u, p_v)$，则称这两棵树同构。

The first and only line of input contains a single integer $n$ ($3 \le n \le 1000$) — the number of vertices in the tree.

输入仅有一行，包含一个整数 $n$（$3 \le n \le 1000$）——树中顶点的数量。

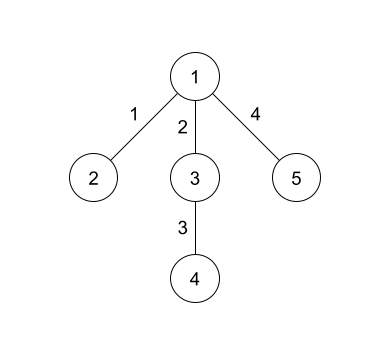
The hidden tree in the example is shown above. The number on the vertices represents the vertex number while the number on the edges represents the edge number.

In the first query, all the edges are set to weight $1$, so the diameter has length $3$ as shown in the diagram.

In the second query, there is $1$ edge between edges $1$ and $3$.

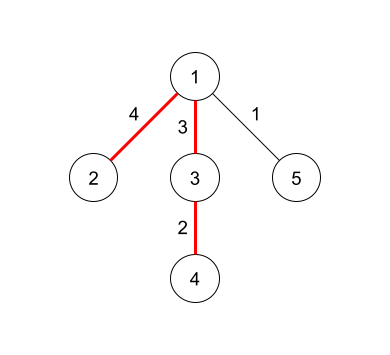
In the third query, the diameter is $9$ by taking edges $1$, $2$ and $3$.

In the fourth query, there are no edges between edges $4$ and $2$.

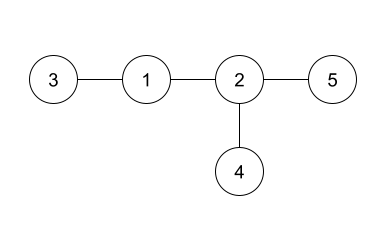
The answer given in the example is shown in the above diagram. Since it is isomorphic to the hidden tree, it is accepted as a correct answer. Note that the edges can be printed in any order.

示例中隐藏的树如上图所示。顶点上的数字表示顶点编号，边上的数字表示边编号。

在第一次查询中，所有边的权重均设为 $1$，因此直径长度为 $3$，如图所示。

在第二次查询中，边 $1$ 与边 $3$ 之间存在 $1$ 条边。

在第三次查询中，选取边 $1$、$2$ 和 $3$ 可使直径达到 $9$。

在第四次查询中，边 $4$ 与边 $2$ 之间不存在边。

示例中给出的答案如上图所示。由于该树与隐藏树同构，因此被接受为正确答案。注意：边的输出顺序可以任意。