CF1889F.Doremy's Average Tree

普及/提高-

通过率：0%

AC君温馨提醒

该题目为【codeforces】题库的题目，您提交的代码将被提交至codeforces进行远程评测，并由ACGO抓取测评结果后进行展示。由于远程测评的测评机由其他平台提供，我们无法保证该服务的稳定性，若提交后无反应，请等待一段时间后再进行重试。

题目描述

Doremy has a rooted tree of size $n$ whose root is vertex $r$ . Initially there is a number $w_i$ written on vertex $i$ . Doremy can use her power to perform this operation at most $k$ times:

Choose a vertex $x$ ( $1 \leq x \leq n$ ).
Let $s = \frac{1}{|T|}\sum_{i \in T} w_i$ where $T$ is the set of all vertices in $x$ 's subtree.
For all $i \in T$ , assign $w_i := s$ .

Doremy wants to know what is the lexicographically smallest $^\dagger$ array $w$ after performing all the operations. Can you help her?

If there are multiple answers, you may output any one.

$^\dagger$ For arrays $a$ and $b$ both of length $n$ , $a$ is lexicographically smaller than $b$ if and only if there exist an index $i$ ( $1 \leq i \le n$ ) such that $a_i < b_i$ and for all indices $j$ such that $j<i$ , $a_j=b_j$ is satisfied.

输入格式

The input consists of multiple test cases. The first line contains a single integer $t$ ( $1\le t\le 10^4$ ) — the number of test cases. The description of the test cases follows.

The first line contains three integers $n$ , $r$ , $k$ ( $2 \le n \le 5000$ , $1 \le r \le n$ , $0 \le k \le \min(500,n)$ ).

The second line contains $n$ integers $w_1,w_2,\ldots,w_n$ ( $1 \le w_i \le 10^6$ ).

Each of the next $n-1$ lines contains two integers $u_i$ , $v_i$ ( $1 \leq u_i, v_i \leq n$ ), representing an edge between $u_i$ and $v_i$ .

It is guaranteed that the given edges form a tree.

It is guaranteed that the sum of $n$ does not exceed $50\,000$ .

输出格式

For each test case, In the first line, output a single integer $cnt$ ( $0 \le cnt \le k$ ) — the number of operations you perform.

Then, in the second line output $cnt$ integers $p_1,p_2,\ldots,p_{cnt}$ — $x$ is chosen to be $p_i$ for $i$ -th operation.

If there are multiple answers, you may output any one.

输入输出样例

输入#1

4
6 1 1
1 9 2 6 1 8
1 2
1 3
2 4
3 6
3 5
7 7 2
3 1 3 3 1 1 2
7 1
7 2
7 4
1 5
2 3
4 6
6 5 1
3 1 3 1 1 3
5 3
5 1
5 6
3 4
1 2
3 2 1
1000000 999999 999997
2 1
1 3

输出#1

说明/提示

In the first test case:

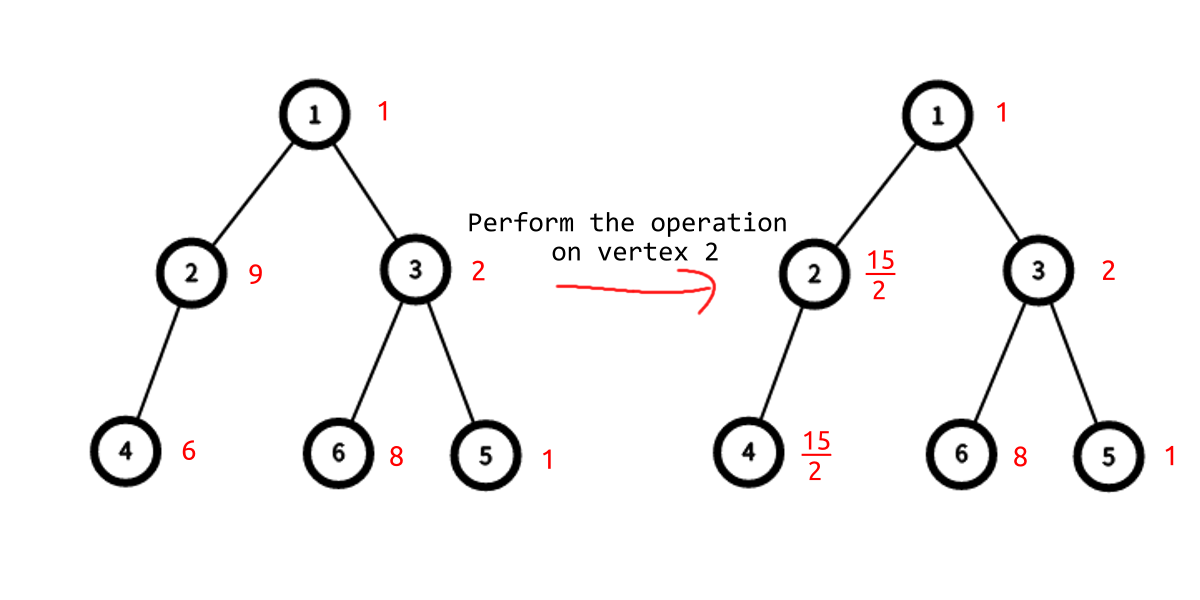
At first $w=[1,9,2,6,1,8]$ . You can choose some vertex $x$ to perform at most one operation.

If $x=1$ , $w=[\frac{9}{2},\frac{9}{2},\frac{9}{2},\frac{9}{2},\frac{9}{2},\frac{9}{2}]$ .
If $x=2$ , $w=[1,\frac{15}{2},2,\frac{15}{2},1,8]$ .
If $x=3$ , $w=[1,9,\frac{11}{3},6,\frac{11}{3},\frac{11}{3}]$ .
If $x \in \{4, 5, 6\}$ , $w=[1,9,2,6,1,8]$ .
If you don't perform any operation, $w=[1,9,2,6,1,8]$ .

$w$ is lexicographically smallest when $x=2$ .

首页