CF1898C.Colorful Grid

Elena has a grid formed by $n$ horizontal lines and $m$ vertical lines. The horizontal lines are numbered by integers from $1$ to $n$ from top to bottom. The vertical lines are numbered by integers from $1$ to $m$ from left to right. For each $x$ and $y$ ($1 \leq x \leq n$, $1 \leq y \leq m$), the notation $(x, y)$ denotes the point at the intersection of the $x$-th horizontal line and $y$-th vertical line.

Two points $(x_1,y_1)$ and $(x_2,y_2)$ are adjacent if and only if $|x_1-x_2| + |y_1-y_2| = 1$.

The grid formed by $n=4$ horizontal lines and $m=5$ vertical lines.

Elena calls a sequence of points $p_1, p_2, \ldots, p_g$ of length $g$ a walk if and only if all the following conditions hold:

• The first point $p_1$ in this sequence is $(1, 1)$.
• The last point $p_g$ in this sequence is $(n, m)$.
• For each $1 \le i \lt g$, the points $p_i$ and $p_{i+1}$ are adjacent.

Note that the walk may contain the same point more than once. In particular, it may contain point $(1, 1)$ or $(n, m)$ multiple times.

There are $n(m-1)+(n-1)m$ segments connecting the adjacent points in Elena's grid. Elena wants to color each of these segments in blue or red color so that there exists a walk $p_1, p_2, \ldots, p_{k+1}$ of length $k+1$ such that

• out of $k$ segments connecting two consecutive points in this walk, no two consecutive segments have the same color (in other words, for each $1 \le i \lt k$, the color of the segment between points $p_i$ and $p_{i+1}$ differs from the color of the segment between points $p_{i+1}$ and $p_{i+2}$).

Please find any such coloring or report that there is no such coloring.

埃琳娜有一个由 $n$ 条水平线和 $m$ 条垂直线构成的网格。水平线从上到下依次编号为 $1$ 到 $n$，垂直线从左到右依次编号为 $1$ 到 $m$。对任意 $x$ 和 $y$（满足 $1 \leq x \leq n$，$1 \leq y \leq m$），记号 $(x, y)$ 表示第 $x$ 条水平线与第 $y$ 条垂直线的交点。

两点 $(x_1,y_1)$ 与 $(x_2,y_2)$ 相邻，当且仅当 $|x_1-x_2| + |y_1-y_2| = 1$。

由 $n=4$ 条水平线和 $m=5$ 条垂直线构成的网格。

埃琳娜称一个长度为 $g$ 的点序列 $p_1, p_2, \ldots, p_g$ 为一条路径（walk），当且仅当满足以下所有条件：

• 该序列的第一个点 $p_1$ 是 $(1, 1)$；
• 该序列的最后一个点 $p_g$ 是 $(n, m)$；
• 对每个 $1 \le i < g$，点 $p_i$ 与 $p_{i+1}$ 相邻。

注意：该路径允许重复经过同一个点。特别地，它可能多次经过点 $(1, 1)$ 或 $(n, m)$。

在埃琳娜的网格中，共有 $n(m-1)+(n-1)m$ 条连接相邻点的线段。埃琳娜希望将每条线段染成蓝色或红色，使得存在一条长度为 $k+1$ 的路径 $p_1, p_2, \ldots, p_{k+1}$，满足：

• 在该路径中连接相邻两点的 $k$ 条线段中，任意两条连续的线段颜色均不相同（即：对每个 $1 \le i < k$，点 $p_i$ 与 $p_{i+1}$ 之间的线段颜色不同于点 $p_{i+1}$ 与 $p_{i+2}$ 之间的线段颜色）。

请构造出任意一种满足要求的染色方案，或判定不存在这样的染色方案。

Each test contains multiple test cases. The first line contains the number of test cases $t$ ($1 \leq t \leq 32$). The description of test cases follows.

The only line of each test case contains three integers $n$, $m$, and $k$ ($3 \leq n,m \leq 16$, $1 \leq k \leq 10^9$) — the dimensions of the grid and the number of segments in the walk Elena is looking for.

每个测试包含多个测试用例。第一行包含测试用例的数量 $t$（$1 \leq t \leq 32$）。随后是各测试用例的描述。

每个测试用例仅有一行，包含三个整数 $n$、$m$ 和 $k$（$3 \leq n,m \leq 16$，$1 \leq k \leq 10^9$）—— 分别表示网格的维度以及 Elena 所寻找的路径中的线段数量。

For each test case, output "NO" if it is not possible to color each of the $n(m-1)+(n-1)m$ segments in blue or red color, so that there exists a walk of length $k+1$ satisfying the condition from the statement.

Otherwise, output in the first line "YES", and then provide the required coloring.

In each of the first $n$ lines of coloring description, output $m-1$ space-separated characters. The $j$-th character in the $i$-th of these $n$ lines should denote the color of the segment between points $(i,j)$ and $(i,j+1)$. Here, use 'B' to denote the blue color and 'R' to denote the red color.

In each of the next $n-1$ lines of coloring description, output $m$ space-separated characters. The $j$-th character in the $i$-th of these $n-1$ lines should denote the color of the segment between points $(i,j)$ and $(i+1,j)$. Similarly, use 'B' to denote the blue color and 'R' to denote the red color.

You can output each letter in the answer in any case (upper or lower). For example, the strings "yEs", "yes", "Yes", and "YES" will be recognized as positive responses, and both 'R' and 'r' are valid notation of red.

对于每个测试用例，若无法将全部 $n(m-1)+(n-1)m$ 条线段染成蓝色或红色，使得存在一条长度为 $k+1$ 的路径满足题目所述条件，则输出 "NO"。

否则，在第一行输出 "YES"，随后给出所要求的染色方案。

在染色方案描述的前 $n$ 行中，每行输出 $m-1$ 个以空格分隔的字符。这 $n$ 行中的第 $i$ 行的第 $j$ 个字符表示连接点 $(i,j)$ 与 $(i,j+1)$ 的线段的颜色。其中，用 'B' 表示蓝色，'R' 表示红色。

在染色方案描述的接下来的 $n-1$ 行中，每行输出 $m$ 个以空格分隔的字符。这 $n-1$ 行中的第 $i$ 行的第 $j$ 个字符表示连接点 $(i,j)$ 与 $(i+1,j)$ 的线段的颜色。同样地，用 'B' 表示蓝色，'R' 表示红色。

答案中每个字母的大小写均可（即大小写不敏感）。例如，字符串 "yEs"、"yes"、"Yes" 和 "YES" 均被视为肯定回答，且 'R' 与 'r' 均为红色的有效表示。

In the first test case, one of the correct answers is shown in the picture below. The color-alternating walk of length $12$ is highlighted.

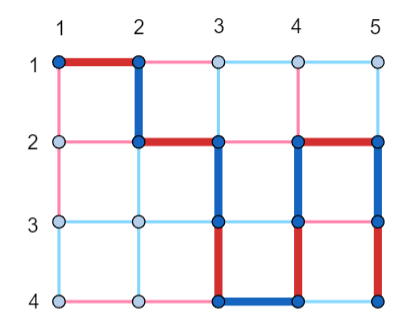In the second and the third test cases, it can be shown that there is no coloring satisfying the condition from the statement.

在第一个测试用例中，一个正确的答案如下图所示。图中高亮显示了一条长度为 $12$ 的颜色交替路径。

在第二个和第三个测试用例中，可以证明不存在满足题目条件的染色方案。