CF1900C.Anji's Binary Tree

Keksic keeps getting left on seen by Anji. Through a mutual friend, he's figured out that Anji really likes binary trees and decided to solve her problem in order to get her attention.

Anji has given Keksic a binary tree with $n$ vertices. Vertex $1$ is the root and does not have a parent. All other vertices have exactly one parent. Each vertex can have up to $2$ children, a left child, and a right child. For each vertex, Anji tells Keksic index of both its left and its right child or tells him that they do not exist.

Additionally, each of the vertices has a letter $s_i$ on it, which is either 'U', 'L' or 'R'.

Keksic begins his journey on the root, and in each move he does the following:

• If the letter on his current vertex is 'U', he moves to its parent. If it doesn't exist, he does nothing.
• If the letter on his current vertex is 'L', he moves to its left child. If it doesn't exist, he does nothing.
• If the letter on his current vertex is 'R', he moves to its right child. If it doesn't exist, he does nothing.

Before his journey, he can perform the following operations: choose any node, and replace the letter written on it with another one. You are interested in the minimal number of operations he needs to do before his journey, such that when he starts his journey, he will reach a leaf at some point. A leaf is a vertex that has no children. It does not matter which leaf he reaches. Note that it does not matter whether he will stay in the leaf, he just needs to move to it. Additionally, note that it does not matter how many times he needs to move before reaching a leaf.

Help Keksic solve Anji's tree so that he can win her heart, and make her come to Čačak.
凯克西奇一直被安吉冷落。通过一个共同的朋友，他发现安吉非常喜欢二叉树，于是决定解决她的问题，以引起她的注意。

Anji 给了 Keksic 一棵有 n
个顶点的二叉树。顶点 1
是根，没有父顶点。所有其他顶点都有一个父顶点。每个顶点最多可以有 2
个子顶点、一个左子顶点和一个右子顶点。对于每个顶点，安吉会告诉凯克西奇它的左子和右子的索引，或者告诉他它们不存在。

此外，每个顶点上都有一个字母 si
，分别是 "U"、"L "或 "R"。

凯克西奇从根部开始他的旅程，在每一步棋中他都会进行以下操作：

如果当前顶点上的字母是 "U"，他就移动到它的父顶点。如果它不存在，他就什么也不做。
如果当前顶点上的字母是 "L"，则移动到其左侧子顶点。如果它不存在，则他什么也不做。
如果当前顶点上的字母是 "R"，则移动到其右边的子顶点。如果它不存在，则他什么也不做。
在移动之前，他可以执行以下操作：选择任意一个节点，并用另一个节点替换写在上面的字母。

我们感兴趣的是，当他开始旅行时，他将在某一点到达一片叶子，那么他在旅行前需要做的操作的最小数目。叶子是一个没有子顶点的顶点。他到达哪片叶子并不重要。需要注意的是，他是否会停留在叶子上并不重要，他只需要移动到叶子上。此外，他需要移动多少次才能到达一片叶子也无关紧要。

帮助 Keksic 解开安吉的树，这样他就能赢得她的芳心，让她来到恰恰克。

Each test consists of multiple test cases. The first line contains a single integer $t$ ( $1 \le t \le 5 \cdot 10^4$ ) — the number of test cases. The description of test cases follows.

The first line of each test case contains a single integer $n$ ( $2 \le n \le 3 \cdot 10^5$ ) — the number of vertices in a tree.

The second line of each test case contains a string $s$ of $n$ characters — characters are written on the vertices. It is guaranteed that $s$ consists only of characters 'U', 'L', and 'R'.

The $i$ -th of the next $n$ lines contains two integers $l_i$ and $r_i$ ( $0 \le l_i, r_i \le n$ ) — indices of left and right child of the vertex $i$ . If $l_i = 0$ , it means that vertex $i$ does not have a left child. If $r_i = 0$ , it means that vertex $i$ does not have a right child. It is guaranteed that this data describes a valid binary tree rooted at $1$ .

It is guaranteed that the sum of $n$ over all test cases does not exceed $3 \cdot 10^5$ .
输入

每个测试由多个测试用例组成。第一行包含一个整数 $t$ ( $1 \leq t \le 5 \cdot 10^4$ )--测试用例数。( $1 \le t \le 5 \cdot 10^4$ ) - 测试用例的数量。测试用例说明如下。

每个测试用例的第一行都包含一个整数 $n$ ( $2 \le n \le 3 \cdot 10^5$ ) - 树的顶点数。

每个测试用例的第二行包含一个由 $n$ 个字符组成的字符串 $s$ - 字符写在顶点上。保证 $s$ 只包含字符 "U"、"L "和 "R"。

接下来 $n$ 行的 $i-th$包含两个整数 $l _i$ 和 $r_i$ ( $0 \leq l_i, r_i \leq n$ )--顶点 $i$ 的左右子节点的索引。如果是 l _ i = 0 ，则表示顶点 $i$ 没有左子顶点。如果是 $r_i = 0$ ，则表示顶点 $i$ 没有右子顶点。可以保证，这些数据描述了一棵有效的二叉树，其根位于 $1$ 。

保证所有测试用例中 $n$ 的总和不超过 $3 \cdot 10^5$ 。

For each test case, output a single integer — the minimal number of operations Keksic needs to do to reach a leaf.
输出

对于每个测试用例，输出一个整数，即 Keksic 到达叶子所需的最小操作数。

In the first test case, vertex $1$ has $2$ as its left child and $3$ as its right child. Vertices $2$ and $3$ do not have children and are therefore leaves. As 'L' is written on vertex $1$ , Keksic will go to vertex $2$ , therefore he has to do no operations.

In the second test case, vertex $1$ has $3$ as its left child and $2$ as its right child. Vertices $2$ and $3$ are leaves. As 'U' is written on vertex $1$ , Keksic needs to change it to either 'L' or 'R' in order for him to reach a leaf.

In the third case, vertex $1$ has only a right child, which is vertex $2$ . As 'L' is written on it, Keksic needs to change it to 'R', otherwise he would be stuck on vertex $1$ .

In the fourth case, he can change $3$ characters so that letters on the vertices are "LURL", which makes him reach vertex $2$ .

In the fifth case, there are $3$ leaves, $3$ , $6$ and $7$ . To reach either leaf $6$ or leaf $7$ , he needs to change $2$ characters. However, if he changes character on vertex $1$ to 'R', he will reach leaf $3$ , therefore the answer is $1$ .

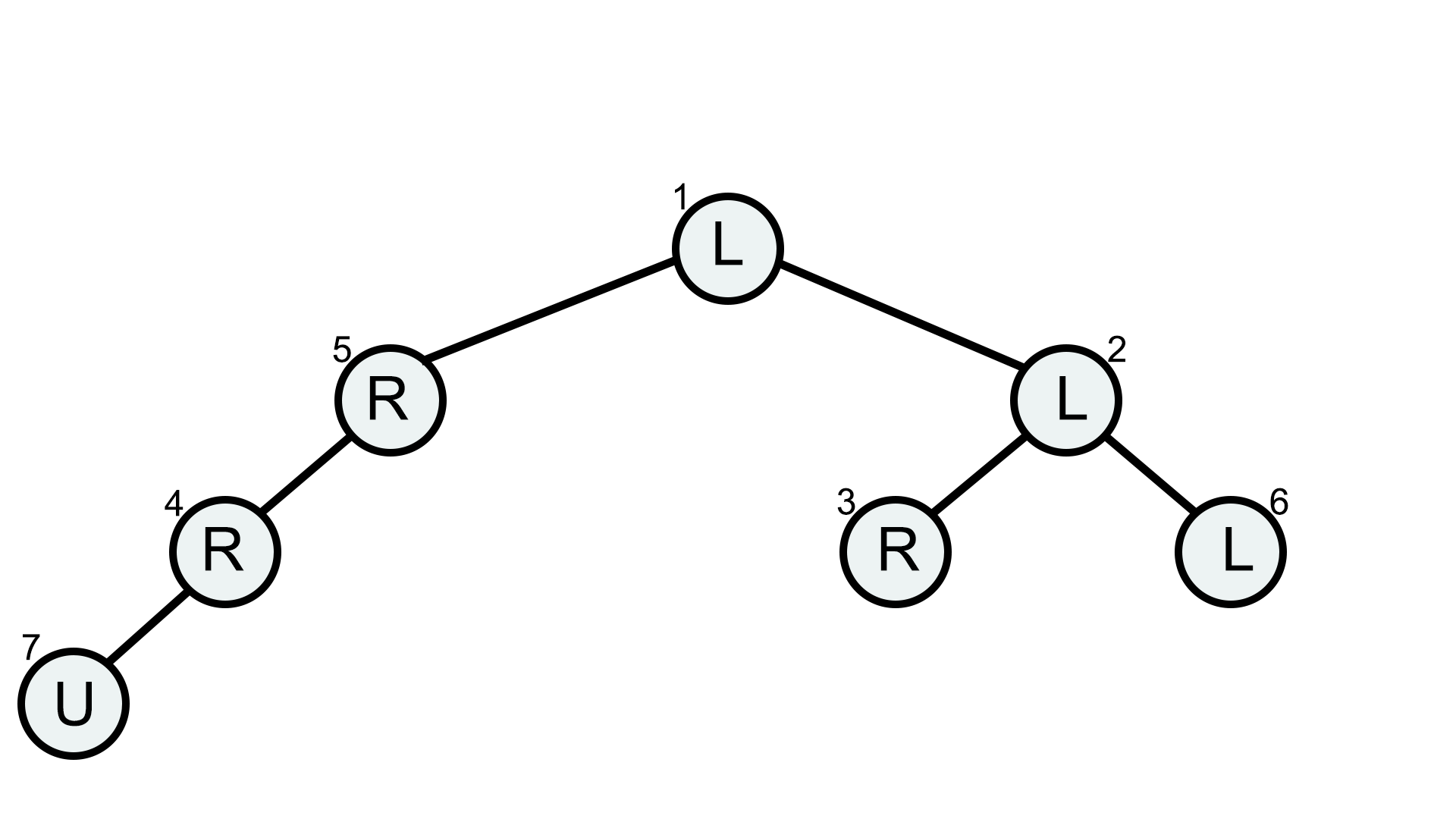The initial tree in test case 5.
备注

在第一个测试案例中，顶点 $1$ 的左子顶点是 $2$ ，右子顶点是 $3$ 。顶点 $2$ 和 $3$ 没有子顶点，因此是叶子。由于 "L "写在顶点 $1$ 上，Keksic 将前往顶点 $2$ ，因此他无需进行任何操作。

在第二个测试案例中，顶点 $1$ 的左子顶点为 $3$ ，右子顶点为 $2$ 。顶点 $2$ 和 $3$ 是叶子。由于顶点 $1$ 上写有 "U"，因此克希奇需要将其改为 "L "或 "R "才能到达叶子。

在第三种情况中，顶点 $1$ 只有一个右子顶点，即顶点 $2$ 。由于顶点 $1$ 上写有 "L"，因此凯克西奇需要将其改为 "R"，否则他将被困在顶点 $1$ 上。

在第四种情况下，他可以更改 $3$ 个字符，这样顶点上的字母就是 "LURL"，从而到达顶点 $2$ 。

在第五种情况中，有 $3$ 片叶子、 $3$ 、 $6$ 和 $7$ 。要到达叶 $6$ 或叶 $7$ ，他需要更改 $2$ 个字符。然而，如果他将顶点 $1$ 上的字符更改为'R'，他将到达叶子 $3$ ，因此答案是 $1$ 。

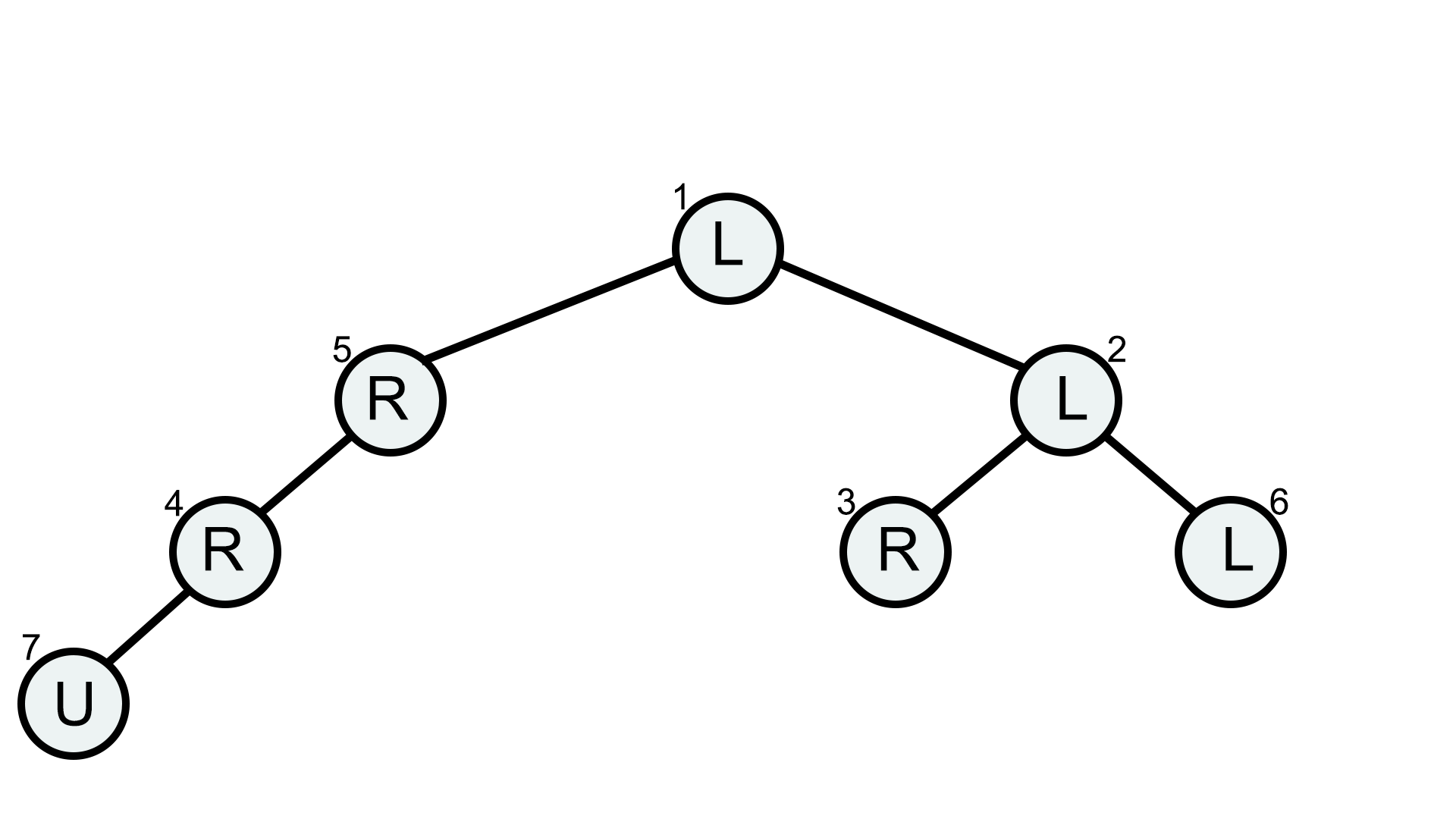测试用例 5 中的初始树。