CF1905E.One-X

In this sad world full of imperfections, ugly segment trees exist.

A segment tree is a tree where each node represents a segment and has its number. A segment tree for an array of $n$ elements can be built in a recursive manner. Let's say function $\operatorname{build}(v,l,r)$ builds the segment tree rooted in the node with number $v$ and it corresponds to the segment $[l,r]$.

Now let's define $\operatorname{build}(v,l,r)$:

• If $l=r$, this node $v$ is a leaf so we stop adding more edges
• Else, we add the edges $(v, 2v)$ and $(v, 2v+1)$. Let $m=\lfloor \frac{l+r}{2} \rfloor$. Then we call $\operatorname{build}(2v,l,m)$ and $\operatorname{build}(2v+1,m+1,r)$.

So, the whole tree is built by calling $\operatorname{build}(1,1,n)$.

Now Ibti will construct a segment tree for an array with $n$ elements. He wants to find the sum of $\operatorname{lca}^\dagger(S)$, where $S$ is a non-empty subset of leaves. Notice that there are exactly $2^n - 1$ possible subsets. Since this sum can be very large, output it modulo $998\,244\,353$.

$^\dagger\operatorname{lca}(S)$ is the number of the least common ancestor for the nodes that are in $S$.

在这个充满缺憾的悲伤世界中，丑陋的线段树确实存在。

线段树是一种树形结构，其中每个节点代表一个区间并拥有一个编号。对于一个包含 $n$ 个元素的数组，其线段树可通过递归方式构建。我们定义函数 $\operatorname{build}(v,l,r)$ 表示以编号为 $v$ 的节点为根、对应区间为 $[l,r]$ 的线段树的构建过程。

下面给出 $\operatorname{build}(v,l,r)$ 的定义：

• 若 $l=r$，则该节点 $v$ 是叶子节点，不再添加新的边；
• 否则，添加两条边 $(v, 2v)$ 和 $(v, 2v+1)$；令 $m=\lfloor \frac{l+r}{2} \rfloor$，然后递归调用 $\operatorname{build}(2v,l,m)$ 和 $\operatorname{build}(2v+1,m+1,r)$。

因此，整棵线段树通过调用 $\operatorname{build}(1,1,n)$ 构建而成。

现在 Ibti 将为一个含 $n$ 个元素的数组构造一棵线段树。他希望求出所有非空叶子节点子集 $S$ 对应的 $\operatorname{lca}^\dagger(S)$ 的总和。注意这样的子集共有 $2^n - 1$ 个。由于该总和可能非常大，请将结果对 $998\,244\,353$ 取模后输出。

$^\dagger\operatorname{lca}(S)$ 表示集合 $S$ 中所有节点的最近公共祖先（LCA）的编号。

Each test consists of multiple test cases. The first line contains a single integer $t$ ($1 \le t \le 10^3$) — the number of test cases. The description of the test cases follows.

The first line of each test case contains a single integer $n$ ($2 \le n \le 10^{18}$) — the length of the array for which the segment tree is built.

每个测试包含多个测试用例。第一行包含一个整数 $t$（$1 \le t \le 10^3$），表示测试用例的数量。随后是各测试用例的描述。

每个测试用例的第一行包含一个整数 $n$（$2 \le n \le 10^{18}$），表示为其构建线段树的数组长度。

For each test case, output a single integer — the required sum modulo $998\,244\,353$.

对于每个测试用例，输出一个整数——所求的和对 $998\,244\,353$ 取模的结果。

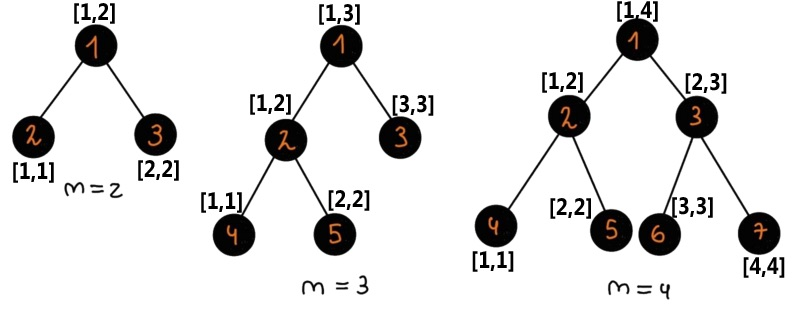In the first test case:

Let's look at all subsets of leaves.

• $\operatorname{lca}({2})=2$;
• $\operatorname{lca}({3})=3$;
• $\operatorname{lca}({2,3})=1$.

Thus, the answer is $2+3+1=6$.

In the second test case:

Let's look at all subsets of leaves.

• $\operatorname{lca}({4})=4$;
• $\operatorname{lca}({5})=5$;
• $\operatorname{lca}({3})=3$;
• $\operatorname{lca}({4,5})=2$;
• $\operatorname{lca}({4,3})=1$;
• $\operatorname{lca}({5,3})=1$;
• $\operatorname{lca}({4,5,3})=1$;

Thus, the answer is $4+5+3+2+1+1+1=17$.

在第一个测试用例中：

我们考察所有叶子节点的子集。

• $\operatorname{lca}({2})=2$；
• $\operatorname{lca}({3})=3$；
• $\operatorname{lca}({2,3})=1$。

因此，答案为 $2+3+1=6$。

在第二个测试用例中：

我们考察所有叶子节点的子集。

• $\operatorname{lca}({4})=4$；
• $\operatorname{lca}({5})=5$；
• $\operatorname{lca}({3})=3$；
• $\operatorname{lca}({4,5})=2$；
• $\operatorname{lca}({4,3})=1$；
• $\operatorname{lca}({5,3})=1$；
• $\operatorname{lca}({4,5,3})=1$；

因此，答案为 $4+5+3+2+1+1+1=17$。