CF1872B.The Corridor or There and Back Again

You are in a corridor that extends infinitely to the right, divided into square rooms. You start in room $1$, proceed to room $k$, and then return to room $1$. You can choose the value of $k$. Moving to an adjacent room takes $1$ second.

Additionally, there are $n$ traps in the corridor: the $i$-th trap is located in room $d_i$ and will be activated $s_i$ seconds after you enter the room $\boldsymbol{d_i}$. Once a trap is activated, you cannot enter or exit a room with that trap.

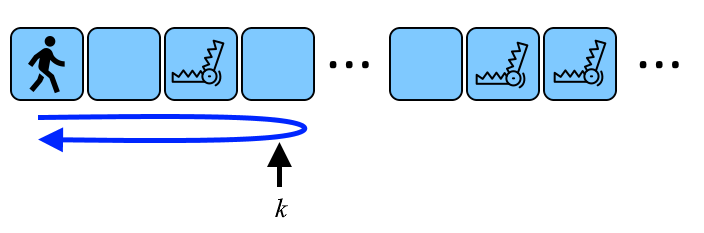A schematic representation of a possible corridor and your path to room $k$ and back.

Determine the maximum value of $k$ that allows you to travel from room $1$ to room $k$ and then return to room $1$ safely.

For instance, if $n=1$ and $d_1=2, s_1=2$, you can proceed to room $k=2$ and return safely (the trap will activate at the moment $1+s_1=1+2=3$, it can't prevent you to return back). But if you attempt to reach room $k=3$, the trap will activate at the moment $1+s_1=1+2=3$, preventing your return (you would attempt to enter room $2$ on your way back at second $3$, but the activated trap would block you). Any larger value for $k$ is also not feasible. Thus, the answer is $k=2$.

你位于一条向右无限延伸的走廊中，走廊被划分为若干个正方形房间。你从第 $1$ 个房间出发，前往第 $k$ 个房间，再返回第 $1$ 个房间。你可以自由选择 $k$ 的值。每次移动到相邻房间耗时 $1$ 秒。

此外，走廊中存在 $n$ 个陷阱：第 $i$ 个陷阱位于第 $d_i$ 个房间，并在你进入房间 $\boldsymbol{d_i}$ 后 $s_i$ 秒被触发。一旦陷阱被触发，你就无法再进入或离开带有该陷阱的房间。

走廊及你前往房间 $k$ 并返回路径的一种示意图。

请确定最大的 $k$ 值，使得你能安全地从房间 $1$ 出发到达房间 $k$，再返回房间 $1$。

例如，若 $n=1$，且 $d_1=2,\, s_1=2$，则你可以安全地前往房间 $k=2$ 并返回（陷阱将在时刻 $1+s_1=1+2=3$ 触发，此时你早已返回，因此不影响返程）。但若尝试到达房间 $k=3$，陷阱仍会在时刻 $1+s_1=1+2=3$ 触发，从而阻碍你返程（你在返程途中将于第 $3$ 秒重新进入房间 $2$，而此时陷阱已激活，将阻止你通行）。任何更大的 $k$ 值也同样不可行。因此答案为 $k=2$。

The first line of the input contains an integer $t$ ($1 \le t \le 1000$) — the number of test cases.

The descriptions of the test cases follow.

The first line of each test case description contains an integer $n$ ($1 \le n \le 100$) — the number of traps.

The following $n$ lines of each test case description present two integers $d_i$ and $s_i$ ($1 \le d_i, s_i \le 200$) — the parameters of a trap (you must leave room $d_i$ strictly before $s_i$ seconds have passed since entering this room). It's possible for multiple traps to occupy a single room (the values of $d_i$ can be repeated).

输入的第一行包含一个整数 $t$（$1 \le t \le 1000$），表示测试用例的数量。

随后是各测试用例的描述。

每个测试用例描述的第一行包含一个整数 $n$（$1 \le n \le 100$），表示陷阱的数量。

每个测试用例描述的接下来 $n$ 行，每行包含两个整数 $d_i$ 和 $s_i$（$1 \le d_i, s_i \le 200$），表示一个陷阱的参数（你必须在进入该房间后的 $s_i$ 秒严格过去之前，留出 $d_i$ 的空间）。多个陷阱可能位于同一房间中（即 $d_i$ 的值可能重复）。

For each test case, print the maximum value of $k$ that allows you to travel to room $k$ and return to room $1$ without encountering an active trap.

对于每个测试用例，输出最大的 $k$ 值，使得你可以前往房间 $k$ 并返回房间 $1$，且途中不触发任何活跃陷阱。

The first test case is explained in the problem statement above.

In the second test case, the second trap prevents you from achieving $k\ge6$. If $k\ge6$, the second trap will activate at the moment $3+s_2=3+3=6$ (the time you enter room $4$ plus $s_2$). In the case of $k\ge6$, you will return to room $4$ at time $7$ or later. The trap will be active at that time. It can be shown that room $k=5$ can be reached without encountering an active trap.

In the third test case, you can make it to room $299$ and then immediately return to room $1$.

第一个测试用例已在题目描述中说明。

在第二个测试用例中，第二个陷阱阻止你达到 $k\ge6$。若 $k\ge6$，则第二个陷阱将在时刻 $3+s_2=3+3=6$ 触发（即你进入房间 $4$ 的时刻加上 $s_2$）。当 $k\ge6$ 时，你将在时刻 $7$ 或更晚返回房间 $4$，此时该陷阱处于激活状态。可以证明：房间 $k=5$ 可以在不遭遇任何激活陷阱的情况下到达。

在第三个测试用例中，你可以抵达房间 $299$，然后立即返回房间 $1$。