CF1873E.Building an Aquarium

You love fish, that's why you have decided to build an aquarium. You have a piece of coral made of $n$ columns, the $i$ -th of which is $a_i$ units tall. Afterwards, you will build a tank around the coral as follows:

• Pick an integer $h \geq 1$ — the height of the tank. Build walls of height $h$ on either side of the tank.
• Then, fill the tank up with water so that the height of each column is $h$ , unless the coral is taller than $h$ ; then no water should be added to this column.

For example, with $a=[3,1,2,4,6,2,5]$ and a height of $h=4$ , you will end up using a total of $w=8$ units of water, as shown. 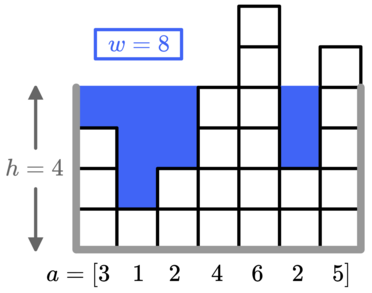You can use at most $x$ units of water to fill up the tank, but you want to build the biggest tank possible. What is the largest value of $h$ you can select?

The first line contains a single integer $t$ ( $1 \leq t \leq 10^4$ ) — the number of test cases.

The first line of each test case contains two positive integers $n$ and $x$ ( $1 \leq n \leq 2 \cdot 10^5$ ; $1 \leq x \leq 10^9$ ) — the number of columns of the coral and the maximum amount of water you can use.

The second line of each test case contains $n$ space-separated integers $a_i$ ( $1 \leq a_i \leq 10^9$ ) — the heights of the coral.

The sum of $n$ over all test cases doesn't exceed $2 \cdot 10^5$ .

For each test case, output a single positive integer $h$ ( $h \geq 1$ ) — the maximum height the tank can have, so you need at most $x$ units of water to fill up the tank.

We have a proof that under these constraints, such a value of $h$ always exists.

The first test case is pictured in the statement. With $h=4$ we need $8$ units of water, but if $h$ is increased to $5$ we need $13$ units of water, which is more than $x=9$ . So $h=4$ is optimal.

In the second test case, we can pick $h=4$ and add $3$ units to each column, using a total of $9$ units of water. It can be shown that this is optimal.

In the third test case, we can pick $h=2$ and use all of our water, so it is optimal.