CF1842E.Tenzing and Triangle

There are $n$ pairwise-distinct points and a line $x+y=k$ on a two-dimensional plane. The $i$ -th point is at $(x_i,y_i)$ . All points have non-negative coordinates and are strictly below the line. Alternatively, $0 \leq x_i,y_i, x_i+y_i < k$ .

Tenzing wants to erase all the points. He can perform the following two operations:

1. Draw triangle: Tenzing will choose two non-negative integers $a$ , $b$ that satisfy $a+b<k$ , then all points inside the triangle formed by lines $x=a$ , $y=b$ and $x+y=k$ will be erased. It can be shown that this triangle is an isosceles right triangle. Let the side lengths of the triangle be $l$ , $l$ and $\sqrt 2 l$ respectively. Then, the cost of this operation is $l \cdot A$ .The blue area of the following picture describes the triangle with $a=1,b=1$ with cost $=1\cdot A$ .

   

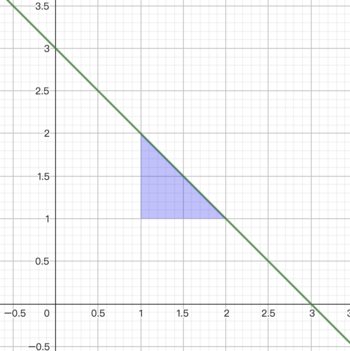
2. Erase a specific point: Tenzing will choose an integer $i$ that satisfies $1 \leq i \leq n$ and erase the point $i$ . The cost of this operation is $c_i$ .

Help Tenzing find the minimum cost to erase all of the points.

The first line of the input contains three integers $n$ , $k$ and $A$ ( $1\leq n,k\leq 2\cdot 10^5$ , $1\leq A\leq 10^4$ ) — the number of points, the coefficient describing the hypotenuse of the triangle and the coefficient describing the cost of drawing a triangle.

The following $n$ lines of the input the $i$ -th line contains three integers $x_i,y_i,c_i$ ( $0\leq x_i,y_i,x_i+y_i< k$ , $1\leq c_i\leq 10^4$ ) — the coordinate of the $i$ -th points and the cost of erasing it using the second operation. It is guaranteed that the coordinates are pairwise distinct.

Output a single integer —the minimum cost needed to erase all of the points.

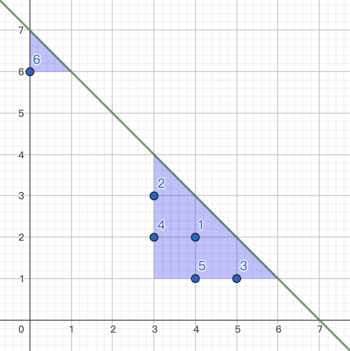
The picture of the first example:

Tenzing do the following operations:

1. draw a triangle with $a=3,b=2$ , the cost $=1\cdot A=1$ .
2. erase the first point, the cost $=1$ .
3. erase the second point, the cost $=1$ .
4. erase the third point, the cost $=1$ .

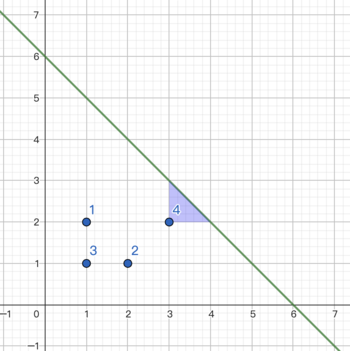The picture of the second example: