CF1843D.Apple Tree

Timofey has an apple tree growing in his garden; it is a rooted tree of $n$ vertices with the root in vertex $1$ (the vertices are numbered from $1$ to $n$ ). A tree is a connected graph without loops and multiple edges.

This tree is very unusual — it grows with its root upwards. However, it's quite normal for programmer's trees.

The apple tree is quite young, so only two apples will grow on it. Apples will grow in certain vertices (these vertices may be the same). After the apples grow, Timofey starts shaking the apple tree until the apples fall. Each time Timofey shakes the apple tree, the following happens to each of the apples:

Let the apple now be at vertex $u$ .

• If a vertex $u$ has a child, the apple moves to it (if there are several such vertices, the apple can move to any of them).
• Otherwise, the apple falls from the tree.

It can be shown that after a finite time, both apples will fall from the tree.

Timofey has $q$ assumptions in which vertices apples can grow. He assumes that apples can grow in vertices $x$ and $y$ , and wants to know the number of pairs of vertices ( $a$ , $b$ ) from which apples can fall from the tree, where $a$ — the vertex from which an apple from vertex $x$ will fall, $b$ — the vertex from which an apple from vertex $y$ will fall. Help him do this.

The first line contains integer $t$ ( $1 \leq t \leq 10^4$ ) — the number of test cases.

The first line of each test case contains integer $n$ ( $2 \leq n \leq 2 \cdot 10^5$ ) — the number of vertices in the tree.

Then there are $n - 1$ lines describing the tree. In line $i$ there are two integers $u_i$ and $v_i$ ( $1 \leq u_i, v_i \leq n$ , $u_i \ne v_i$ ) — edge in tree.

The next line contains a single integer $q$ ( $1 \leq q \leq 2 \cdot 10^5$ ) — the number of Timofey's assumptions.

Each of the next $q$ lines contains two integers $x_i$ and $y_i$ ( $1 \leq x_i, y_i \leq n$ ) — the supposed vertices on which the apples will grow for the assumption $i$ .

It is guaranteed that the sum of $n$ does not exceed $2 \cdot 10^5$ . Similarly, It is guaranteed that the sum of $q$ does not exceed $2 \cdot 10^5$ .

For each Timofey's assumption output the number of ordered pairs of vertices from which apples can fall from the tree if the assumption is true on a separate line.

In the first example:

• For the first assumption, there are two possible pairs of vertices from which apples can fall from the tree: $(4, 4), (5, 4)$ .
• For the second assumption there are also two pairs: $(5, 4), (5, 5)$ .
• For the third assumption there is only one pair: $(4, 4)$ .
• For the fourth assumption, there are $4$ pairs: $(4, 4), (4, 5), (5, 4), (5, 5)$ .

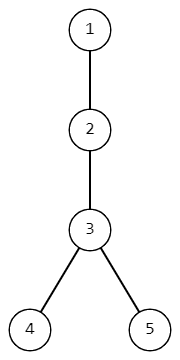Tree from the first example.For the second example, there are $4$ of possible pairs of vertices from which apples can fall: $(2, 3), (2, 2), (3, 2), (3, 3)$ . For the second assumption, there is only one possible pair: $(2, 3)$ . For the third assumption, there are two pairs: $(3, 2), (3, 3)$ .