CF1845B.Come Together

Bob and Carol hanged out with Alice the whole day, but now it's time to go home. Alice, Bob and Carol live on an infinite 2D grid in cells $A$ , $B$ , and $C$ respectively. Right now, all of them are in cell $A$ .

If Bob (or Carol) is in some cell, he (she) can move to one of the neighboring cells. Two cells are called neighboring if they share a side. For example, the cell $(3, 5)$ has four neighboring cells: $(2, 5)$ , $(4, 5)$ , $(3, 6)$ and $(3, 4)$ .

Bob wants to return to the cell $B$ , Carol — to the cell $C$ . Both of them want to go along the shortest path, i. e. along the path that consists of the minimum possible number of cells. But they would like to walk together as well.

What is the maximum possible number of cells that Bob and Carol can walk together if each of them walks home using one of the shortest paths?

The first line contains the single integer $t$ ( $1 \le t \le 10^4$ ) — the number of test cases.

The first line of each test case contains two integers $x_A$ and $y_A$ ( $1 \le x_A, y_A \le 10^8$ ) — the position of cell $A$ , where both Bob and Carol are right now.

The second line contains two integers $x_B$ and $y_B$ ( $1 \le x_B, y_B \le 10^8$ ) — the position of cell $B$ (Bob's house).

The third line contains two integers $x_C$ and $y_C$ ( $1 \le x_C, y_C \le 10^8$ ) — the position of cell $C$ (Carol's house).

Additional constraint on the input: the cells $A$ , $B$ , and $C$ are pairwise distinct in each test case.

For each test case, print the single integer — the maximum number of cells Bob and Carol can walk together if each of them goes home along one of the shortest paths.

In all pictures, red color denotes cells belonging only to Bob's path, light blue color — cells belonging only to Carol's path, and dark blue color — cells belonging to both paths.

One of the optimal routes for the first test case is shown below:

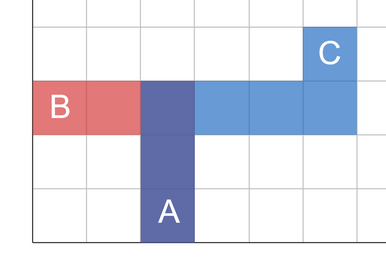Bob's route contains $5$ cells, Carol's route — $7$ cells, and they will visit $3$ cells together.The optimal answer for the second test case is shown below:

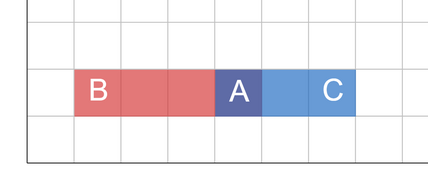Bob's route contains $4$ cells, Carol's route — $3$ cells, and they will visit only $1$ cell together.One of the optimal answers for the third test case is shown below:

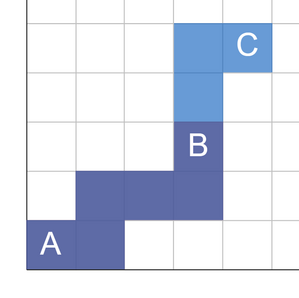Bob's route contains $6$ cells, Carol's route — $9$ cells, and they will visit $6$ cells together.