CF1846E1.Rudolf and Snowflakes (simple version)

This is a simple version of the problem. The only difference is that in this version $n \le 10^6$.

One winter morning, Rudolf was looking thoughtfully out the window, watching the falling snowflakes. He quickly noticed a certain symmetry in the configuration of the snowflakes. And like a true mathematician, Rudolf came up with a mathematical model of a snowflake.

He defined a snowflake as an undirected graph constructed according to the following rules:

• Initially, the graph has only one vertex.
• Then, more vertices are added to the graph. The initial vertex is connected by edges to $k$ new vertices ($k \gt 1$).
• Each vertex that is connected to only one other vertex is connected by edges to $k$ more new vertices. This step should be done at least once.

The smallest possible snowflake for $k = 4$ is shown in the figure.

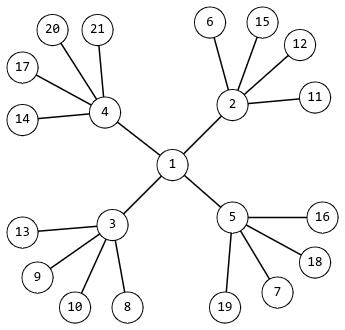After some mathematical research, Rudolf realized that such snowflakes may not have any number of vertices. Help Rudolf check if a snowflake with $n$ vertices can exist.

这是一个该问题的简化版本，唯一的区别在于本版本中 $n \le 10^6$。

一个冬日清晨，鲁道夫若有所思地望着窗外，观察着飘落的雪花。他很快注意到雪花构型中存在某种对称性。作为一名真正的数学家，鲁道夫据此提出了雪花的数学模型。

他将雪花定义为一个按如下规则构造的无向图：

• 初始时，图中仅含一个顶点；
• 随后向图中添加更多顶点：初始顶点与 $k$ 个新顶点（$k > 1$）分别连边；
• 每个仅与一个其他顶点相邻的顶点，均需再与 $k$ 个新顶点分别连边；此步骤至少执行一次。

当 $k = 4$ 时，最小可能的雪花如图所示。

经过一些数学研究，鲁道夫意识到此类雪花的顶点数并非任意正整数均可取。请帮助鲁道夫判断：是否存在一个含 $n$ 个顶点的雪花。

The first line of the input contains an integer $t$ ($1 \le t \le 10^4$) — the number of test cases.

Then follow the descriptions of the test cases.

The first line of each test case contains an integer $n$ ($1 \le n \le 10^6$) — the number of vertices for which it is necessary to check the existence of a snowflake.

输入的第一行包含一个整数 $t$（$1 \le t \le 10^4$）—— 测试用例的数量。

随后是各测试用例的描述。

每个测试用例的第一行包含一个整数 $n$（$1 \le n \le 10^6$）—— 需要检查是否存在雪花结构的顶点数量。

Output $t$ lines, each of which is the answer to the corresponding test case — "YES" if there exists such $k \gt 1$ for which a snowflake with the given number of vertices can be constructed; "NO" otherwise.

输出 $t$ 行，每行对应一个测试用例的答案：若存在满足 $k \gt 1$ 的整数 $k$，使得能够构造出具有给定顶点数的雪花图形，则输出 "YES"；否则输出 "NO"。