CF1824E.LuoTianyi and Cartridge

LuoTianyi is watching the anime Made in Abyss. She finds that making a Cartridge is interesting. To describe the process of making a Cartridge more clearly, she abstracts the original problem and gives you the following problem.

You are given a tree $T$ consisting of $n$ vertices. Each vertex has values $a_i$ and $b_i$ and each edge has values $c_j$ and $d_j$.

Now you are aim to build a tree $T'$ as follows:

• First, select $p$ vertices from $T$ ($p$ is a number chosen by yourself) as the vertex set $S'$ of $T'$.
• Next, select $p-1$ edges from $T$ one by one (you cannot select one edge more than once).
• May you have chosen the $j$-th edge connects vertices $x_j$ and $y_j$ with values $(c_j,d_j)$, then you can choose two vertices $u$ and $v$ in $S'$ that satisfy the edge $(x_j,y_j)$ is contained in the simple path from $u$ to $v$ in $T$, and link $u$ and $v$ in $T'$ by the edge with values $(c_j,d_j)$ ($u$ and $v$ shouldn't be contained in one connected component before in $T'$).

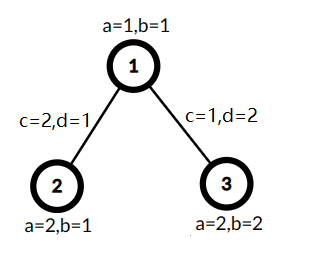A tree with three vertices, $\min(A,C)=1,B+D=7$, the cost is $7$.

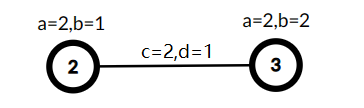Selected vertices $2$ and $3$ as $S'$, used the edge $(1,2)$ with $c_j = 2$ and $d_j = 1$ to link this vertices, now $\min(A,C)=2,B+D=4$, the cost is $8$.

Let $A$ be the minimum of values $a_i$ in $T'$ and $C$ be the minimum of values $c_i$ in $T'$. Let $B$ be the sum of $b_i$ in $T'$ and $D$ be the sum of values $d_i$ in $T'$. Let $\min(A, C) \cdot (B + D)$ be the cost of $T'$. You need to find the maximum possible cost of $T'$.

洛天依正在观看动画《来自深渊》。她发现制作“卡带”十分有趣。为了更清晰地描述制作卡带的过程，她对原问题进行了抽象，并向你提出了如下问题。

给定一棵包含 $n$ 个顶点的树 $T$。每个顶点 $i$ 具有值 $a_i$ 和 $b_i$；每条边 $j$ 具有值 $c_j$ 和 $d_j$。

现在你需要构造一棵新树 $T'$，具体步骤如下：

• 首先，从 $T$ 中任选 $p$ 个顶点（$p$ 由你自己决定）作为 $T'$ 的顶点集 $S'$；
• 接着，从 $T$ 中逐条选出 $p-1$ 条边（每条边至多被选一次）；
• 假设你第 $j$ 次选择的边连接顶点 $x_j$ 与 $y_j$，其对应值为 $(c_j, d_j)$，则你可在 $S'$ 中任选两个顶点 $u$ 和 $v$，满足：在 $T$ 中，边 $(x_j, y_j)$ 位于 $u$ 到 $v$ 的唯一简单路径上；然后在 $T'$ 中用一条权值为 $(c_j, d_j)$ 的边连接 $u$ 与 $v$（注意：在加入该边前，$u$ 与 $v$ 在 $T'$ 中不能属于同一连通分量）。

一棵含三个顶点的树，$\min(A,C)=1,\ B+D=7$，代价为 $7$。

选取顶点 $2$ 和 $3$ 作为 $S'$，使用边 $(1,2)$（其 $c_j = 2$、$d_j = 1$）连接这两个顶点，此时 $\min(A,C)=2,\ B+D=4$，代价为 $8$。

令 $A$ 表示 $T'$ 中所有顶点 $a_i$ 值的最小值，$C$ 表示 $T'$ 中所有边 $c_i$ 值的最小值；
令 $B$ 表示 $T'$ 中所有顶点 $b_i$ 值的总和，$D$ 表示 $T'$ 中所有边 $d_i$ 值的总和；
定义 $T'$ 的代价为 $\min(A, C) \cdot (B + D)$。
你需要求出 $T'$ 可能取得的最大代价。

The first line contains one integer $n$ ($3\le n \le 2\cdot 10^5$) — the number of vertices in the tree $T$.

The second line contains $n$ integers $a_1, a_2, \ldots, a_n$ ($1\le a_i\le 2\cdot 10^5$), where the $i$-th integer represents the $a_i$ value of the $i$-th vertex.

The third line contains $n$ integers $b_1, b_2, \ldots, b_n$ ($1\le b_i\le 2\cdot 10^5$), where the $i$-th integer represents the $b_i$ value of the $i$-th vertex.

Then $n-1$ lines follow, the $j$-th of them contains four integers $x_j,y_j,c_j,d_j$ ($1\le x_j,y_j\le n,1\le c_j,d_j\le 2\cdot 10^5$) representing the edge $(x_j,y_j)$ and its values $c_j$ and $d_j$ respectively. It's guaranteed that edges form a tree.

第一行包含一个整数 $n$（$3\le n \le 2\cdot 10^5$）——树 $T$ 的顶点数。

第二行包含 $n$ 个整数 $a_1, a_2, \ldots, a_n$（$1\le a_i\le 2\cdot 10^5$），其中第 $i$ 个整数表示第 $i$ 个顶点的 $a_i$ 值。

第三行包含 $n$ 个整数 $b_1, b_2, \ldots, b_n$（$1\le b_i\le 2\cdot 10^5$），其中第 $i$ 个整数表示第 $i$ 个顶点的 $b_i$ 值。

接下来是 $n-1$ 行，第 $j$ 行包含四个整数 $x_j,y_j,c_j,d_j$（$1\le x_j,y_j\le n,\,1\le c_j,d_j\le 2\cdot 10^5$），表示边 $(x_j,y_j)$ 及其对应的值 $c_j$ 和 $d_j$。保证这些边构成一棵树。

Print a single integer — the maximum possible cost of $T'$.

输出一个整数——$T'$ 的最大可能代价。

The tree from the first example is shown in the statement.

The tree from the second example is shown below:

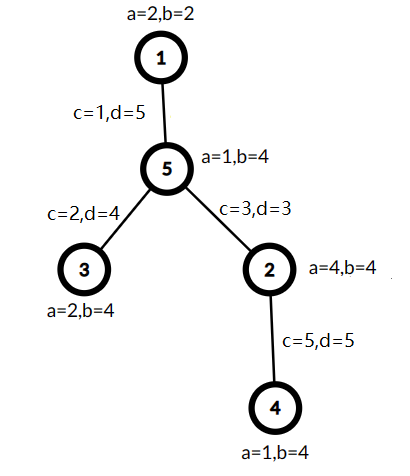$A = 1, B = 18, C = 1, D = 17$, so the cost is $\min(1,1) \cdot (18 + 17) = 35$.

第一个示例中的树如题面所示。

第二个示例中的树如下所示：

$A = 1, B = 18, C = 1, D = 17$，因此代价为 $\min(1,1) \cdot (18 + 17) = 35$。