CF1798C.Candy Store

The store sells $n$ types of candies with numbers from $1$ to $n$ . One candy of type $i$ costs $b_i$ coins. In total, there are $a_i$ candies of type $i$ in the store.

You need to pack all available candies in packs, each pack should contain only one type of candies. Formally, for each type of candy $i$ you need to choose the integer $d_i$ , denoting the number of type $i$ candies in one pack, so that $a_i$ is divided without remainder by $d_i$ .

Then the cost of one pack of candies of type $i$ will be equal to $b_i \cdot d_i$ . Let's denote this cost by $c_i$ , that is, $c_i = b_i \cdot d_i$ .

After packaging, packs will be placed on the shelf. Consider the cost of the packs placed on the shelf, in order $c_1, c_2, \ldots, c_n$ . Price tags will be used to describe costs of the packs. One price tag can describe the cost of all packs from $l$ to $r$ inclusive if $c_l = c_{l+1} = \ldots = c_r$ . Each of the packs from $1$ to $n$ must be described by at least one price tag. For example, if $c_1, \ldots, c_n = [4, 4, 2, 4, 4]$ , to describe all the packs, a $3$ price tags will be enough, the first price tag describes the packs $1, 2$ , the second: $3$ , the third: $4, 5$ .

You are given the integers $a_1, b_1, a_2, b_2, \ldots, a_n, b_n$ . Your task is to choose integers $d_i$ so that $a_i$ is divisible by $d_i$ for all $i$ , and the required number of price tags to describe the values of $c_1, c_2, \ldots, c_n$ is the minimum possible.

For a better understanding of the statement, look at the illustration of the first test case of the first test:

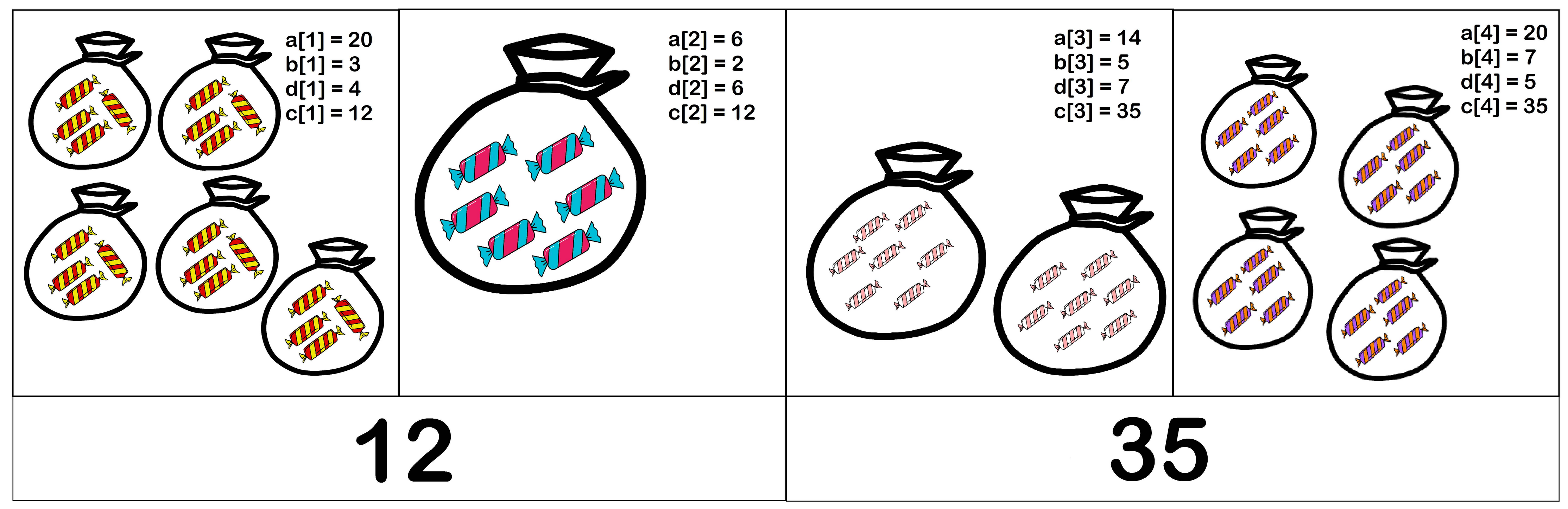Let's repeat the meaning of the notation used in the problem:

$a_i$ — the number of candies of type $i$ available in the store.

$b_i$ — the cost of one candy of type $i$ .

$d_i$ — the number of candies of type $i$ in one pack.

$c_i$ — the cost of one pack of candies of type $i$ is expressed by the formula $c_i = b_i \cdot d_i$ .

Each test contains multiple test cases. The first line contains the number of test cases $t$ ( $1 \le t \le 100\,000$ ). Description of the test cases follows.

The first line of each test case contains a single integer $n$ ( $2 \le n \le 200\,000$ ) — the number of types of candies.

Each of the next $n$ lines of each test case contains two integers $a_i$ and $b_i$ ( $1 \le a_i \le 10^9$ , $1 \le b_i \le 10\,000$ ) — the number of candies and the cost of one candy of type $i$ , respectively.

It is guaranteed that the sum of $n$ over all test cases does not exceed $200\,000$ .

For each test case, output the minimum number of price tags required to describe the costs of all packs of candies in the store.

In the first test case, you can choose $d_1 = 4$ , $d_2 = 6$ , $d_3 = 7$ , $d_4 = 5$ . Then the cost of packs will be equal to $[12, 12, 35, 35]$ . $2$ price tags are enough to describe them, the first price tag for $c_1, c_2$ and the second price tag for $c_3, c_4$ . It can be shown that with any correct choice of $d_i$ , at least $2$ of the price tag will be needed to describe all the packs. Also note that this example is illustrated by a picture in the statement.

In the second test case, with $d_1 = 4$ , $d_2 = 2$ , $d_3 = 10$ , the costs of all packs will be equal to $20$ . Thus, $1$ price tag is enough to describe all the packs. Note that $a_i$ is divisible by $d_i$ for all $i$ , which is necessary condition.

In the third test case, it is not difficult to understand that one price tag can be used to describe $2$ nd, $3$ rd and $4$ th packs. And additionally a price tag for pack $1$ and pack $5$ . Total: $3$ price tags.