CF1675D.Vertical Paths

You are given a rooted tree consisting of $n$ vertices. Vertices are numbered from $1$ to $n$ . Any vertex can be the root of a tree.

A tree is a connected undirected graph without cycles. A rooted tree is a tree with a selected vertex, which is called the root.

The tree is specified by an array of parents $p$ containing $n$ numbers: $p_i$ is a parent of the vertex with the index $i$ . The parent of a vertex $u$ is a vertex that is the next vertex on the shortest path from $u$ to the root. For example, on the simple path from $5$ to $3$ (the root), the next vertex would be $1$ , so the parent of $5$ is $1$ .

The root has no parent, so for it, the value of $p_i$ is $i$ (the root is the only vertex for which $p_i=i$ ).

Find such a set of paths that:

• each vertex belongs to exactly one path, each path can contain one or more vertices;
• in each path each next vertex — is a son of the current vertex (that is, paths always lead down — from parent to son);
• number of paths is minimal.

For example, if $n=5$ and $p=[3, 1, 3, 3, 1]$ , then the tree can be divided into three paths:

1. $3 \rightarrow 1 \rightarrow 5$ (path of $3$ vertices),
2. $4$ (path of $1$ vertices).
3. $2$ (path of $1$ vertices).

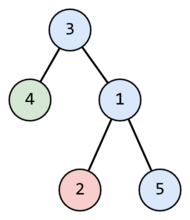Example of splitting a root tree into three paths for $n=5$ , the root of the tree — node $3$ .

The first line of input data contains an integer $t$ ( $1 \le t \le 10^4$ ) — the number of test cases in the test.

Each test case consists of two lines.

The first of them contains an integer $n$ ( $1 \le n \le 2 \cdot 10^5$ ). It is the number of vertices in the tree.

The second line contains $n$ integers $p_1, p_2, \dots, p_n$ ( $1 \le p_i \le n$ ). It is guaranteed that the $p$ array encodes some rooted tree.

It is guaranteed that the sum of the values $n$ over all test cases in the test does not exceed $2 \cdot 10^5$ .

For each test case on the first line, output an integer $m$ — the minimum number of non-intersecting leading down paths that can cover all vertices of the tree.

Then print $m$ pairs of lines containing path descriptions. In the first of them print the length of the path, in the second — the sequence of vertices specifying that path in the order from top to bottom. You can output the paths in any order.

If there are several answers, output any of them.