CF1016F.Road Projects

There are $n$ cities in the country of Berland. Some of them are connected by bidirectional roads in such a way that there exists exactly one path, which visits each road no more than once, between every pair of cities. Each road has its own length. Cities are numbered from $1$ to $n$.

The travelling time between some cities $v$ and $u$ is the total length of the roads on the shortest path from $v$ to $u$.

The two most important cities in Berland are cities $1$ and $n$.

The Berland Ministry of Transport decided to build a single new road to decrease the traffic between the most important cities. However, lots of people are used to the current travelling time between the most important cities, so the new road shouldn't change it too much.

The new road can only be built between such cities $v$ and $u$ that $v \neq u$ and $v$ and $u$ aren't already connected by some road.

They came up with $m$ possible projects. Each project is just the length $x$ of the new road.

Polycarp works as a head analyst at the Berland Ministry of Transport and it's his job to deal with all those $m$ projects. For the $i$-th project he is required to choose some cities $v$ and $u$ to build the new road of length $x_i$ between such that the travelling time between the most important cities is maximal possible.

Unfortunately, Polycarp is not a programmer and no analyst in the world is capable to process all projects using only pen and paper.

Thus, he asks you to help him to calculate the maximal possible travelling time between the most important cities for each project. Note that the choice of $v$ and $u$ can differ for different projects.

伯兰德国有 $n$ 座城市。其中一些城市通过双向道路相连，使得任意两座城市之间都恰好存在一条路径（每条道路至多经过一次）。每条道路都有其自身的长度。城市编号为 $1$ 到 $n$。

城市 $v$ 与 $u$ 之间的通行时间定义为从 $v$ 到 $u$ 的最短路径上所有道路长度的总和。

伯兰德国两个最重要的城市是城市 $1$ 和城市 $n$。

伯兰德交通部决定修建一条新道路，以缓解两个最重要城市之间的交通压力。然而，许多人已习惯当前两个最重要城市之间的通行时间，因此新道路不应使该通行时间发生过大变化。

新道路只能修建在满足以下条件的两座城市 $v$ 和 $u$ 之间：$v \neq u$，且 $v$ 与 $u$ 当前尚未由任何道路直接相连。

他们共提出了 $m$ 个备选方案。每个方案仅指定新道路的长度 $x$。

波利卡普在伯兰德交通部担任首席分析师，处理全部 $m$ 个方案正是他的职责。对于第 $i$ 个方案，他需要选定两座城市 $v$ 和 $u$，并在其间修建一条长度为 $x_i$ 的新道路，使得两个最重要城市之间的通行时间尽可能大。

不幸的是，波利卡普并非程序员，且世界上没有任何一位分析师能单靠纸笔完成全部方案的计算。

因此，他请求你帮助他计算出：对每个方案，两个最重要城市之间所能达到的最大可能通行时间。注意：不同方案所选择的 $v$ 和 $u$ 可以不同。

The first line contains two integers $n$ and $m$ ($3 \le n \le 3 \cdot 10^5$, $1 \le m \le 3 \cdot 10^5$) — the number of cities and the number of projects, respectively.

Each of the next $n - 1$ lines contains three integers $v_i$, $u_i$ and $w_i$ ($1 \le v_i, u_i \le n$, $1 \le w_i \le 10^9$) — the description of the $i$-th road. It is guaranteed that there exists exactly one path, which visits each road no more than once, between every pair of cities.

Each of the next $m$ lines contains a single integer $x_j$ ($1 \le x_j \le 10^9$) — the length of the road for the $j$-th project.

第一行包含两个整数 $n$ 和 $m$（$3 \le n \le 3 \cdot 10^5$，$1 \le m \le 3 \cdot 10^5$）—— 分别表示城市的数量和项目的数量。

接下来的 $n - 1$ 行中，每行包含三个整数 $v_i$、$u_i$ 和 $w_i$（$1 \le v_i, u_i \le n$，$1 \le w_i \le 10^9$）—— 描述第 $i$ 条道路。保证任意两座城市之间均存在唯一一条路径，且该路径上每条道路至多经过一次。

接下来的 $m$ 行中，每行包含一个整数 $x_j$（$1 \le x_j \le 10^9$）—— 表示第 $j$ 个项目的道路长度。

Print $m$ lines, the $j$-th line should contain a single integer — the maximal possible travelling time between the most important cities for the $j$-th project.

输出 $m$ 行，其中第 $j$ 行应包含一个整数——第 $j$ 个项目的最重要城市之间可能的最大旅行时间。

The road network from the first example:

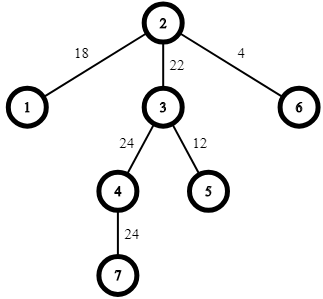
You can build the road with length $1$ between cities $5$ and $6$ to get $83$ as the travelling time between $1$ and $7$ ($1 \rightarrow 2 \rightarrow 6 \rightarrow 5 \rightarrow 3 \rightarrow 4 \rightarrow 7$ $=$ $18 + 4 + 1 + 12 + 24 + 24 = 83$). Other possible pairs of cities will give answers less or equal to $83$.

第一个样例中的道路网络：

你可以在城市 $5$ 和 $6$ 之间修建一条长度为 $1$ 的道路，使得城市 $1$ 与城市 $7$ 之间的通行时间为 $83$（路径为 $1 \rightarrow 2 \rightarrow 6 \rightarrow 5 \rightarrow 3 \rightarrow 4 \rightarrow 7$，对应时间为 $18 + 4 + 1 + 12 + 24 + 24 = 83$）。其余任意一对城市之间修建道路所得的通行时间均不超过 $83$。