A122.棋盘问题
普及+/提高
NOIP提高组
通过率:0%
时间限制:1.00s
内存限制:128MB
题目描述
在N×N的棋盘上(1≤N≤10),填入1,2,…,N2共N2个数,使得任意两个相邻的数之和为素数。
例如:当N=2时,有:
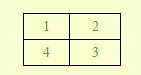
其相邻数的和为素数的有:
1+2,1+4,4+3,2+3
当N=4时,一种可以填写的方案如下:
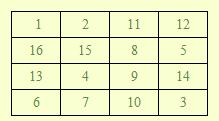
在这里我们约定:左上角的格子里必须填数字1。
输入格式
一个数N。
输出格式
如有多种解,则输出第一行、第一列之和为最小的排列方案;若无解,则输出“NO”。
输入输出样例
输入#1
1
输出#1
NO
输入#2
2
输出#2
1 2 4 3
说明/提示
【题目来源】
NOIP 1997 提高组第一题