CF520C.DNA Alignment

Vasya became interested in bioinformatics. He's going to write an article about similar cyclic DNA sequences, so he invented a new method for determining the similarity of cyclic sequences.

Let's assume that strings s and t have the same length n, then the function h(s, t) is defined as the number of positions in which the respective symbols of s and t are the same. Function h(s, t) can be used to define the function of Vasya distance ρ(s, t):

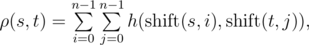where is obtained from string s, by applying left circular shift i times. For example,

ρ("AGC", "CGT") =

h("AGC", "CGT") + h("AGC", "GTC") + h("AGC", "TCG") +

h("GCA", "CGT") + h("GCA", "GTC") + h("GCA", "TCG") +

h("CAG", "CGT") + h("CAG", "GTC") + h("CAG", "TCG") =

1 + 1 + 0 + 0 + 1 + 1 + 1 + 0 + 1 = 6

Vasya found a string s of length n on the Internet. Now he wants to count how many strings t there are such that the Vasya distance from the string s attains maximum possible value. Formally speaking, t must satisfy the equation: .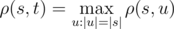

Vasya could not try all possible strings to find an answer, so he needs your help. As the answer may be very large, count the number of such strings modulo 109 + 7.

瓦西娅对生物信息学产生了兴趣。他打算撰写一篇关于相似循环DNA序列的文章，因此发明了一种判定循环序列相似性的新方法。

假设字符串 $s$ 和 $t$ 长度均为 $n$，则函数 $h(s,\,t)$ 定义为 $s$ 与 $t$ 在对应位置上字符相同的个数。利用函数 $h(s,\,t)$ 可定义瓦西娅距离 $\rho(s,\,t)$：

其中 $s^{(i)}$ 表示对字符串 $s$ 进行 $i$ 次左循环移位后所得的字符串。例如，

$\rho(\text{"AGC"},\,\text{"CGT"})\,=$

$h(\text{"AGC"},\,\text{"CGT"})\,+\,h(\text{"AGC"},\,\text{"GTC"})\,+\,h(\text{"AGC"},\,\text{"TCG"})\,+$

$h(\text{"GCA"},\,\text{"CGT"})\,+\,h(\text{"GCA"},\,\text{"GTC"})\,+\,h(\text{"GCA"},\,\text{"TCG"})\,+$

$h(\text{"CAG"},\,\text{"CGT"})\,+\,h(\text{"CAG"},\,\text{"GTC"})\,+\,h(\text{"CAG"},\,\text{"TCG"})\,=$

$1\,+\,1\,+\,0\,+\,0\,+\,1\,+\,1\,+\,1\,+\,0\,+\,1\,=\,6$

瓦西娅在网上找到了一个长度为 $n$ 的字符串 $s$。现在他希望计算满足瓦西娅距离 $\rho(s,\,t)$ 取得最大可能值的字符串 $t$ 的个数。形式化地说，$t$ 必须满足方程：。

瓦西娅无法枚举所有可能的字符串来求解，因此需要你的帮助。由于答案可能非常大，请将结果对 $10^9 + 7$ 取模后输出。

The first line of the input contains a single integer n (1 ≤ n ≤ 105).

The second line of the input contains a single string of length n, consisting of characters "ACGT".

输入的第一行包含一个整数 $n$（$1 ≤ n ≤ 10^5$）。

输入的第二行包含一个长度为 $n$ 的字符串，仅由字符 "ACGT" 组成。

Print a single number — the answer modulo 109 + 7.

输出一个数字——答案对 $10^9 + 7$ 取模的结果。

Please note that if for two distinct strings _t_1 and _t_2 values ρ(s, _t_1) и ρ(s, _t_2) are maximum among all possible t, then both strings must be taken into account in the answer even if one of them can be obtained by a circular shift of another one.

In the first sample, there is ρ("C", "C") = 1, for the remaining strings t of length 1 the value of ρ(s, t) is 0.

In the second sample, ρ("AG", "AG") = ρ("AG", "GA") = ρ("AG", "AA") = ρ("AG", "GG") = 4.

In the third sample, ρ("TTT", "TTT") = 27

请注意，如果对于两个不同的字符串 $t_1$ 和 $t_2$，$\rho(s,\,t_1)$ 与 $\rho(s,\,t_2)$ 均在所有可能的 $t$ 中取到最大值，则答案中必须同时包含这两个字符串，即使其中一个字符串可通过另一个字符串的循环移位得到。

在第一个样例中，有 $\rho(\texttt{"C"},\,\texttt{"C"}) = 1$，而对于其余所有长度为 1 的字符串 $t$，$\rho(s,\,t)$ 的值均为 0。

在第二个样例中，$\rho(\texttt{"AG"},\,\texttt{"AG"}) = \rho(\texttt{"AG"},\,\texttt{"GA"}) = \rho(\texttt{"AG"},\,\texttt{"AA"}) = \rho(\texttt{"AG"},\,\texttt{"GG"}) = 4$。

在第三个样例中，$\rho(\texttt{"TTT"},\,\texttt{"TTT"}) = 27$