CF482C.Game with Strings

You play the game with your friend. The description of this game is listed below.

Your friend creates n distinct strings of the same length m and tells you all the strings. Then he randomly chooses one of them. He chooses strings equiprobably, i.e. the probability of choosing each of the n strings equals . You want to guess which string was chosen by your friend.

In order to guess what string your friend has chosen, you are allowed to ask him questions. Each question has the following form: «What character stands on position pos in the string you have chosen?» A string is considered guessed when the answers to the given questions uniquely identify the string. After the string is guessed, you stop asking questions.

You do not have a particular strategy, so as each question you equiprobably ask about a position that hasn't been yet mentioned. Your task is to determine the expected number of questions needed to guess the string chosen by your friend.

你和朋友一起玩这个游戏，游戏规则如下：

朋友构造了 $n$ 个长度均为 $m$ 的互不相同的字符串，并将所有这些字符串都告诉你。然后他从中等概率地随机选择其中一个字符串；即每个字符串被选中的概率均为 。你的目标是猜出朋友所选的是哪一个字符串。

为了猜出朋友选择的字符串，你可以向他提问。每次提问的形式为：“你在所选字符串中，位置为 pos 处的字符是什么？” 当所提问题的答案唯一确定了某个字符串时，即认为该字符串已被成功猜出；此时你将停止提问。

你没有特定的提问策略，因此每次提问时，你都在尚未询问过的位置中等概率地随机选择一个位置进行提问。你的任务是：计算为猜出朋友所选字符串所需的期望提问次数。

The first line contains a single integer n (1 ≤ n ≤ 50) — the number of strings your friend came up with.

The next n lines contain the strings that your friend has created. It is guaranteed that all the strings are distinct and only consist of large and small English letters. Besides, the lengths of all strings are the same and are between 1 to 20 inclusive.

第一行包含一个整数 $n$（$1 \leq n \leq 50$）—— 表示你的朋友构造的字符串数量。

接下来的 $n$ 行包含你的朋友构造的字符串。保证所有字符串互不相同，且仅由大小写英文字母组成。此外，所有字符串的长度均相同，且在 $1$ 到 $20$（含）之间。

Print the single number — the expected value. Your answer will be considered correct if its absolute or relative error doesn't exceed 10 - 9.

输出单个数字——期望值。如果您的答案的绝对或相对误差不超过 $10^{-9}$，则视为正确。

In the first sample the strings only differ in the character in the third position. So only the following situations are possible:

• you guess the string in one question. The event's probability is ;
• you guess the string in two questions. The event's probability is · = (as in this case the first question should ask about the position that is other than the third one);
• you guess the string in three questions. The event's probability is · · = ;

Thus, the expected value is equal to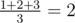

In the second sample we need at most two questions as any pair of questions uniquely identifies the string. So the expected number of questions is .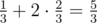

In the third sample whatever position we ask about in the first question, we immediately identify the string.

在第一个样例中，两个字符串仅在第三个位置的字符上不同。因此，仅有以下几种情况可能发生：

• 你通过一次提问就猜中字符串。该事件的概率为 ；
• 你通过两次提问猜中字符串。该事件的概率为 · = （此时第一次提问所询问的位置必须不是第三个位置）；
• 你通过三次提问猜中字符串。该事件的概率为 · · = ；

因此，期望值等于

在第二个样例中，最多需要两次提问，因为任意两个位置的提问均可唯一确定该字符串。因此，提问次数的期望值为 。

在第三个样例中，无论第一次提问询问哪一个位置，均可立即确定该字符串。