CF482D.Random Function and Tree

You have a rooted tree consisting of n vertices. Let's number them with integers from 1 to n inclusive. The root of the tree is the vertex 1. For each i > 1 direct parent of the vertex i is p__i. We say that vertex i is child for its direct parent p__i.

You have initially painted all the vertices with red color. You like to repaint some vertices of the tree. To perform painting you use the function paint that you call with the root of the tree as an argument. Here is the pseudocode of this function:

count = 0 // global integer variable

rnd() { // this function is used in paint code
return 0 or 1 equiprobably
}

paint(s) {
if (count is even) then paint s with white color
else paint s with black color

count = count + 1

if rnd() = 1 then children = [array of vertex s children in ascending order of their numbers]
else children = [array of vertex s children in descending order of their numbers]

for child in children { // iterating over children array
if rnd() = 1 then paint(child) // calling paint recursively
}
}

As a result of this function, some vertices may change their colors to white or black and some of them may remain red.

Your task is to determine the number of distinct possible colorings of the vertices of the tree. We will assume that the coloring is possible if there is a nonzero probability to get this coloring with a single call of paint(1). We assume that the colorings are different if there is a pair of vertices that are painted with different colors in these colorings. Since the required number may be very large, find its remainder of division by 1000000007 (109 + 7).

你有一棵包含 $n$ 个顶点的有根树。我们将这些顶点用 $1$ 到 $n$ 的整数编号（含端点）。树的根为顶点 $1$。对每个 $i > 1$，顶点 $i$ 的直接父节点为 $p_i$。我们称顶点 $i$ 是其直接父节点 $p_i$ 的一个子节点。

初始时，所有顶点均被涂成红色。你喜欢对树中的一些顶点重新着色。为执行着色操作，你调用函数 paint，并以树的根作为参数。该函数的伪代码如下：

count = 0 // 全局整型变量   

rnd() { // 此函数在 paint 代码中使用  
    return 0 或 1，概率均等  
}  
  
paint(s) {  
    if (count 为偶数) then 将 s 涂成白色  
    else 将 s 涂成黑色  
  
    count = count + 1  
   
    if rnd() = 1 then children = [s 的子节点数组，按编号升序排列]  
    else children = [s 的子节点数组，按编号降序排列]  
  
    for child in children { // 遍历 children 数组  
        if rnd() = 1 then paint(child) // 递归调用 paint  
    }  
}  

该函数执行后，部分顶点的颜色可能变为白色或黑色，而其余顶点可能保持红色。

你的任务是确定树的顶点可能产生的不同着色方案总数。若某一种着色方案在单次调用 paint(1) 过程中具有非零概率被生成，则认为该着色方案是可行的。我们认为两种着色方案不同，当且仅当存在至少一个顶点，在这两种方案中被涂成了不同颜色。由于答案可能非常大，请输出其对 $1000000007$（即 $10^9 + 7$）取模的结果。

The first line contains a single integer n (2 ≤ n ≤ 105) — the number of vertexes in the tree.

The second line contains n - 1 integers _p_2, _p_3, ..., p__n (1 ≤ p__i < i). Number p__i is the parent of vertex i.

第一行包含一个整数 $n$（$2 \leq n \leq 10^5$）——树中顶点的数量。

第二行包含 $n-1$ 个整数 $p_2, p_3, \ldots, p_n$（$1 \leq p_i < i$）。其中 $p_i$ 表示顶点 $i$ 的父节点。

Print a single integer — the answer to the problem modulo 1000000007 (109 + 7)

输出一个整数——该问题答案对 1000000007（$10^9 + 7$）取模的结果。

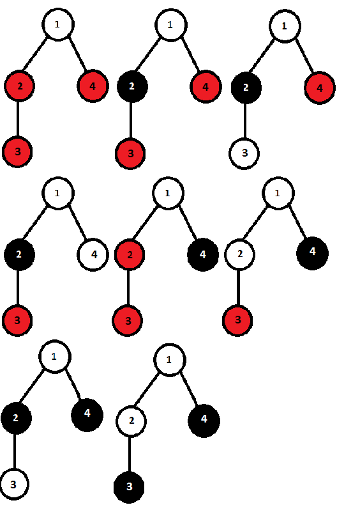
All possible coloring patterns of the first sample are given below.

第一个样例的所有可能的涂色方案如下所示。