CF488B.Candy Boxes
普及/提高-
通过率:0%
AC君温馨提醒
该题目为【codeforces】题库的题目,您提交的代码将被提交至codeforces进行远程评测,并由ACGO抓取测评结果后进行展示。由于远程测评的测评机由其他平台提供,我们无法保证该服务的稳定性,若提交后无反应,请等待一段时间后再进行重试。
题目描述
There is an old tradition of keeping 4 boxes of candies in the house in Cyberland. The numbers of candies are special if their arithmetic mean, their median and their range are all equal. By definition, for a set x1,x2,x3,x4 ( x1<=x2<=x3<=x4 ) arithmetic mean is  , median is
, median is 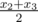 and range is x4−x1 . The arithmetic mean and median are not necessary integer. It is well-known that if those three numbers are same, boxes will create a "debugging field" and codes in the field will have no bugs.
and range is x4−x1 . The arithmetic mean and median are not necessary integer. It is well-known that if those three numbers are same, boxes will create a "debugging field" and codes in the field will have no bugs.
For example, 1,1,3,3 is the example of 4 numbers meeting the condition because their mean, median and range are all equal to 2 .
Jeff has 4 special boxes of candies. However, something bad has happened! Some of the boxes could have been lost and now there are only n ( 0<=n<=4 ) boxes remaining. The i -th remaining box contains ai candies.
Now Jeff wants to know: is there a possible way to find the number of candies of the 4−n missing boxes, meeting the condition above (the mean, median and range are equal)?
输入格式
There is an old tradition of keeping 4 boxes of candies in the house in Cyberland. The numbers of candies are special if their arithmetic mean, their median and their range are all equal. By definition, for a set x1,x2,x3,x4 ( x1<=x2<=x3<=x4 ) arithmetic mean is  , median is
, median is 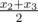 and range is x4−x1 . The arithmetic mean and median are not necessary integer. It is well-known that if those three numbers are same, boxes will create a "debugging field" and codes in the field will have no bugs.
and range is x4−x1 . The arithmetic mean and median are not necessary integer. It is well-known that if those three numbers are same, boxes will create a "debugging field" and codes in the field will have no bugs.
For example, 1,1,3,3 is the example of 4 numbers meeting the condition because their mean, median and range are all equal to 2 .
Jeff has 4 special boxes of candies. However, something bad has happened! Some of the boxes could have been lost and now there are only n ( 0<=n<=4 ) boxes remaining. The i -th remaining box contains ai candies.
Now Jeff wants to know: is there a possible way to find the number of candies of the 4−n missing boxes, meeting the condition above (the mean, median and range are equal)?
输出格式
There is an old tradition of keeping 4 boxes of candies in the house in Cyberland. The numbers of candies are special if their arithmetic mean, their median and their range are all equal. By definition, for a set x1,x2,x3,x4 ( x1<=x2<=x3<=x4 ) arithmetic mean is  , median is
, median is 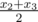 and range is x4−x1 . The arithmetic mean and median are not necessary integer. It is well-known that if those three numbers are same, boxes will create a "debugging field" and codes in the field will have no bugs.
and range is x4−x1 . The arithmetic mean and median are not necessary integer. It is well-known that if those three numbers are same, boxes will create a "debugging field" and codes in the field will have no bugs.
For example, 1,1,3,3 is the example of 4 numbers meeting the condition because their mean, median and range are all equal to 2 .
Jeff has 4 special boxes of candies. However, something bad has happened! Some of the boxes could have been lost and now there are only n ( 0<=n<=4 ) boxes remaining. The i -th remaining box contains ai candies.
Now Jeff wants to know: is there a possible way to find the number of candies of the 4−n missing boxes, meeting the condition above (the mean, median and range are equal)?
输入输出样例
输入#1
2 1 1
输出#1
YES 3 3
输入#2
3 1 1 1
输出#2
NO
输入#3
4 1 2 2 3
输出#3
YES
说明/提示
For the first sample, the numbers of candies in 4 boxes can be 1,1,3,3 . The arithmetic mean, the median and the range of them are all 2 .
For the second sample, it's impossible to find the missing number of candies.
In the third example no box has been lost and numbers satisfy the condition.
You may output b in any order.