CF496A.Minimum Difficulty
普及/提高-
通过率:0%
AC君温馨提醒
该题目为【codeforces】题库的题目,您提交的代码将被提交至codeforces进行远程评测,并由ACGO抓取测评结果后进行展示。由于远程测评的测评机由其他平台提供,我们无法保证该服务的稳定性,若提交后无反应,请等待一段时间后再进行重试。
题目描述
Mike is trying rock climbing but he is awful at it.
There are n holds on the wall, i -th hold is at height ai off the ground. Besides, let the sequence ai increase, that is, ai<ai+1 for all i from 1 to n−1 ; we will call such sequence a track. Mike thinks that the track a1 , ..., an has difficulty 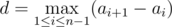 . In other words, difficulty equals the maximum distance between two holds that are adjacent in height.
. In other words, difficulty equals the maximum distance between two holds that are adjacent in height.
Today Mike decided to cover the track with holds hanging on heights a1 , ..., an . To make the problem harder, Mike decided to remove one hold, that is, remove one element of the sequence (for example, if we take the sequence (1,2,3,4,5) and remove the third element from it, we obtain the sequence (1,2,4,5) ). However, as Mike is awful at climbing, he wants the final difficulty (i.e. the maximum difference of heights between adjacent holds after removing the hold) to be as small as possible among all possible options of removing a hold. The first and last holds must stay at their positions.
Help Mike determine the minimum difficulty of the track after removing one hold.
输入格式
Mike is trying rock climbing but he is awful at it.
There are n holds on the wall, i -th hold is at height ai off the ground. Besides, let the sequence ai increase, that is, ai<ai+1 for all i from 1 to n−1 ; we will call such sequence a track. Mike thinks that the track a1 , ..., an has difficulty 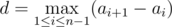 . In other words, difficulty equals the maximum distance between two holds that are adjacent in height.
. In other words, difficulty equals the maximum distance between two holds that are adjacent in height.
Today Mike decided to cover the track with holds hanging on heights a1 , ..., an . To make the problem harder, Mike decided to remove one hold, that is, remove one element of the sequence (for example, if we take the sequence (1,2,3,4,5) and remove the third element from it, we obtain the sequence (1,2,4,5) ). However, as Mike is awful at climbing, he wants the final difficulty (i.e. the maximum difference of heights between adjacent holds after removing the hold) to be as small as possible among all possible options of removing a hold. The first and last holds must stay at their positions.
Help Mike determine the minimum difficulty of the track after removing one hold.
输出格式
Print a single number — the minimum difficulty of the track after removing a single hold.
输入输出样例
输入#1
3 1 4 6
输出#1
5
输入#2
5 1 2 3 4 5
输出#2
2
输入#3
5 1 2 3 7 8
输出#3
4
说明/提示
In the first sample you can remove only the second hold, then the sequence looks like (1,6) , the maximum difference of the neighboring elements equals 5.
In the second test after removing every hold the difficulty equals 2.
In the third test you can obtain sequences (1,3,7,8) , (1,2,7,8) , (1,2,3,8) , for which the difficulty is 4, 5 and 5, respectively. Thus, after removing the second element we obtain the optimal answer — 4.