CF500B.New Year Permutation
普及/提高-
通过率:0%
AC君温馨提醒
该题目为【codeforces】题库的题目,您提交的代码将被提交至codeforces进行远程评测,并由ACGO抓取测评结果后进行展示。由于远程测评的测评机由其他平台提供,我们无法保证该服务的稳定性,若提交后无反应,请等待一段时间后再进行重试。
题目描述
User ainta has a permutation p1,p2,...,pn . As the New Year is coming, he wants to make his permutation as pretty as possible.
Permutation a1,a2,...,an is prettier than permutation b1,b2,...,bn , if and only if there exists an integer k ( 1<=k<=n ) where a1=b1,a2=b2,...,ak−1=bk−1 and a_{k}<b_{k} all holds.
As known, permutation p is so sensitive that it could be only modified by swapping two distinct elements. But swapping two elements is harder than you think. Given an n×n binary matrix A , user ainta can swap the values of pi and pj ( 1<=i,j<=n , i=j ) if and only if Ai,j=1 .
Given the permutation p and the matrix A , user ainta wants to know the prettiest permutation that he can obtain.
输入格式
The first line contains an integer n ( 1<=n<=300 ) — the size of the permutation p .
The second line contains n space-separated integers p1,p2,...,pn — the permutation p that user ainta has. Each integer between 1 and n occurs exactly once in the given permutation.
Next n lines describe the matrix A . The i -th line contains n characters '0' or '1' and describes the i -th row of A . The j -th character of the i -th line Ai,j is the element on the intersection of the i -th row and the j -th column of A. It is guaranteed that, for all integers i,j where 1<=i<j<=n , Ai,j=Aj,i holds. Also, for all integers i where 1<=i<=n , Ai,i=0 holds.
输出格式
In the first and only line, print n space-separated integers, describing the prettiest permutation that can be obtained.
输入输出样例
输入#1
7 5 2 4 3 6 7 1 0001001 0000000 0000010 1000001 0000000 0010000 1001000
输出#1
1 2 4 3 6 7 5
输入#2
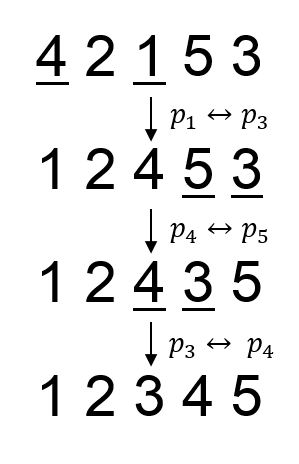
5 4 2 1 5 3 00100 00011 10010 01101 01010
输出#2
1 2 3 4 5
说明/提示
In the first sample, the swap needed to obtain the prettiest permutation is: (p1,p7) .
In the second sample, the swaps needed to obtain the prettiest permutation is (p1,p3),(p4,p5),(p3,p4) .
 A permutation p is a sequence of integers p1,p2,...,pn , consisting of n distinct positive integers, each of them doesn't exceed n . The i -th element of the permutation p is denoted as pi . The size of the permutation p is denoted as n .
A permutation p is a sequence of integers p1,p2,...,pn , consisting of n distinct positive integers, each of them doesn't exceed n . The i -th element of the permutation p is denoted as pi . The size of the permutation p is denoted as n .