CF505B.Mr. Kitayuta's Colorful Graph

Mr. Kitayuta has just bought an undirected graph consisting of n vertices and m edges. The vertices of the graph are numbered from 1 to n. Each edge, namely edge i, has a color c__i, connecting vertex a__i and b__i.

Mr. Kitayuta wants you to process the following q queries.

In the i-th query, he gives you two integers — u__i and v__i.

Find the number of the colors that satisfy the following condition: the edges of that color connect vertex u__i and vertex v__i directly or indirectly.

小野寺先生刚刚购买了一个由 $n$ 个顶点和 $m$ 条边构成的无向图。图中的顶点编号为 $1$ 到 $n$。每条边（即第 $i$ 条边）具有颜色 $c_i$，并连接顶点 $a_i$ 和 $b_i$。

小野寺先生希望你处理以下 $q$ 个查询。

在第 $i$ 个查询中，他会给出两个整数 $u_i$ 和 $v_i$。

请找出满足如下条件的颜色种数：该颜色的所有边（仅考虑该颜色的边构成的子图）能够使顶点 $u_i$ 和顶点 $v_i$ 直接或间接连通。

The first line of the input contains space-separated two integers — n and m (2 ≤ n ≤ 100, 1 ≤ m ≤ 100), denoting the number of the vertices and the number of the edges, respectively.

The next m lines contain space-separated three integers — a__i, b__i (1 ≤ a__i < b__i ≤ n) and c__i (1 ≤ c__i ≤ m). Note that there can be multiple edges between two vertices. However, there are no multiple edges of the same color between two vertices, that is, if i ≠ j, (a__i, b__i, c__i) ≠ (a__j, b__j, c__j).

The next line contains a integer — q (1 ≤ q ≤ 100), denoting the number of the queries.

Then follows q lines, containing space-separated two integers — u__i and v__i (1 ≤ u__i, v__i ≤ n). It is guaranteed that u__i ≠ v__i.

输入的第一行包含两个用空格分隔的整数 $n$ 和 $m$（$2 \leq n \leq 100$，$1 \leq m \leq 100$），分别表示顶点数和边数。

接下来的 $m$ 行每行包含三个用空格分隔的整数 $a_i$、$b_i$（$1 \leq a_i < b_i \leq n$）和 $c_i$（$1 \leq c_i \leq m$）。注意：两个顶点之间可能存在多条边。但任意两个顶点之间不会存在两条颜色相同的边，即若 $i \neq j$，则 $(a_i,\,b_i,\,c_i) \neq (a_j,\,b_j,\,c_j)$。

下一行包含一个整数 $q$（$1 \leq q \leq 100$），表示查询次数。

随后是 $q$ 行，每行包含两个用空格分隔的整数 $u_i$ 和 $v_i$（$1 \leq u_i,\,v_i \leq n$）。保证 $u_i \neq v_i$。

For each query, print the answer in a separate line.

对于每个查询，在单独的一行中输出答案。

Let's consider the first sample.

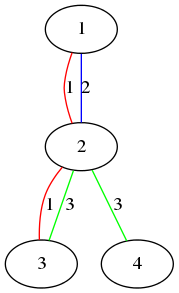The figure above shows the first sample.

• Vertex 1 and vertex 2 are connected by color 1 and 2.
• Vertex 3 and vertex 4 are connected by color 3.
• Vertex 1 and vertex 4 are not connected by any single color.

我们来考虑第一个样例。

上图展示了第一个样例。

• 顶点 1 和顶点 2 通过颜色 1 和颜色 2 相连。
• 顶点 3 和顶点 4 通过颜色 3 相连。
• 顶点 1 和顶点 4 之间不存在某种单一颜色的路径相连。