CF453D.Little Pony and Elements of Harmony

The Elements of Harmony are six supernatural artifacts representing subjective aspects of harmony. They are arguably the most powerful force in Equestria. The inside of Elements of Harmony can be seen as a complete graph with n vertices labeled from 0 to n - 1, where n is a power of two, equal to 2_m_.

The energy in Elements of Harmony is in constant movement. According to the ancient book, the energy of vertex u in time i (e__i[u]) equals to:

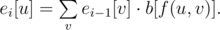Here b[] is the transformation coefficient — an array of m + 1 integers and f(u, v) is the number of ones in the binary representation of number (u xor v).

Given the transformation coefficient and the energy distribution at time 0 (_e_0[]). Help Twilight Sparkle predict the energy distribution at time t (e__t[]). The answer can be quite large, so output it modulo p.

和谐之元是六件代表和谐主观层面的超自然神器，它们可以说是小马国最强大的力量。和谐之元的内部结构可视为一个具有 $n$ 个顶点（编号从 $0$ 到 $n-1$）的完全图，其中 $n$ 是 $2$ 的幂，即 $n = 2^m$。

和谐之元中的能量始终处于持续流动状态。根据古籍记载，顶点 $u$ 在时刻 $i$ 的能量 $e_i[u]$ 满足如下公式：

其中 $b[]$ 是变换系数——一个长度为 $m+1$ 的整数数组，而 $f(u, v)$ 表示数 $u \oplus v$ 的二进制表示中 $1$ 的个数。

已知变换系数 $b[]$ 以及初始时刻（$t=0$）的能量分布 $e_0[]$，请帮助暮光闪闪预测时刻 $t$ 的能量分布 $e_t[]$。答案可能非常大，请对 $p$ 取模后输出。

The first line contains three integers m, t and p (1 ≤ m ≤ 20; 0 ≤ t ≤ 1018; 2 ≤ p ≤ 109). The following line contains n (n = 2_m_) integers _e_0[i] (1 ≤ _e_0[i] ≤ 109; 0 ≤ i < n). The next line contains m + 1 integers b[i] (0 ≤ b[i] ≤ 109; 0 ≤ i ≤ m).

第一行包含三个整数 $m$、$t$ 和 $p$（$1 \le m \le 20$；$0 \le t \le 10^{18}$；$2 \le p \le 10^9$）。
接下来一行包含 $n$（$n = 2^m$）个整数 $e_0[i]$（$1 \le e_0[i] \le 10^9$；$0 \le i < n$）。
再下一行包含 $m+1$ 个整数 $b[i]$（$0 \le b[i] \le 10^9$；$0 \le i \le m$）。

Output n lines, the i-th line must contain a single integer e__t[i] modulo p.

输出 n 行，其中第 i 行必须包含一个整数 e__t[i] 对 p 取模的结果。