CF444A.DZY Loves Physics

DZY loves Physics, and he enjoys calculating density.

Almost everything has density, even a graph. We define the density of a non-directed graph (nodes and edges of the graph have some values) as follows:

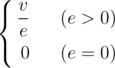where v is the sum of the values of the nodes, e is the sum of the values of the edges.

Once DZY got a graph G, now he wants to find a connected induced subgraph G' of the graph, such that the density of G' is as large as possible.

An induced subgraph G'(V', E') of a graph G(V, E) is a graph that satisfies:

• ;
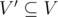• edge 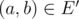if and only if 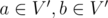, and edge ;
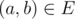• the value of an edge in G' is the same as the value of the corresponding edge in G, so as the value of a node.

Help DZY to find the induced subgraph with maximum density. Note that the induced subgraph you choose must be connected.

DZY 热爱物理，也乐于计算密度。

几乎所有事物都有密度，甚至图（graph）也不例外。我们定义一个无向图（其节点与边均具有某些权值）的密度如下：

其中 $v$ 表示所选节点权值之和，$e$ 表示所选边权值之和。

DZY 得到了一张图 $G$，现在他希望从中找出一个连通的诱导子图 $G'$，使得 $G'$ 的密度尽可能大。

图 $G(V, E)$ 的一个诱导子图 $G'(V', E')$ 是满足以下条件的图：

• ；
• 边 $(u, v) \in E'$ 当且仅当 $u, v \in V'$ 且 $(u, v) \in E$；
• $G'$ 中每条边的权值与其在 $G$ 中对应边的权值相同，每个节点的权值亦同。

请帮助 DZY 找出密度最大的诱导子图。注意：你所选出的诱导子图必须是连通的。

The first line contains two space-separated integers n (1 ≤ n ≤ 500), 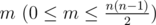. Integer n represents the number of nodes of the graph G, m represents the number of edges.

The second line contains n space-separated integers x__i (1 ≤ x__i ≤ 106), where x__i represents the value of the i-th node. Consider the graph nodes are numbered from 1 to n.

Each of the next m lines contains three space-separated integers a__i, b__i, c__i (1 ≤ a__i < b__i ≤ n; 1 ≤ c__i ≤ 103), denoting an edge between node a__i and b__i with value c__i. The graph won't contain multiple edges.

第一行包含两个以空格分隔的整数 $n$（$1 \leq n \leq 500$）、。整数 $n$ 表示图 $G$ 的节点数，$m$ 表示边数。

第二行包含 $n$ 个以空格分隔的整数 $x_i$（$1 \leq x_i \leq 10^6$），其中 $x_i$ 表示第 $i$ 个节点的值。图的节点编号为 $1$ 到 $n$。

接下来的 $m$ 行每行包含三个以空格分隔的整数 $a_i,\,b_i,\,c_i$（$1 \leq a_i < b_i \leq n$；$1 \leq c_i \leq 10^3$），表示一条连接节点 $a_i$ 与 $b_i$、权值为 $c_i$ 的边。该图不含重边。

Output a real number denoting the answer, with an absolute or relative error of at most 10 - 9.

输出一个实数作为答案，其绝对或相对误差不超过 $10^{-9}$。

In the first sample, you can only choose an empty subgraph, or the subgraph containing only node 1.

In the second sample, choosing the whole graph is optimal.

在第一个样例中，你只能选择空子图，或仅包含节点 1 的子图。

在第二个样例中，选择整个图是最优的。