CF372E.Drawing Circles is Fun

There are a set of points S on the plane. This set doesn't contain the origin O(0, 0), and for each two distinct points in the set A and B, the triangle OAB has strictly positive area.

Consider a set of pairs of points (_P_1, _P_2), (_P_3, _P_4), ..., (P_2_k - 1, P_2_k). We'll call the set good if and only if:

• k ≥ 2.
• All P__i are distinct, and each P__i is an element of S.
• For any two pairs (P_2_i - 1, P_2_i) and (P_2_j - 1, P_2_j), the circumcircles of triangles OP_2_i - 1_P_2_j_ - 1 and OP_2_i__P_2_j have a single common point, and the circumcircle of triangles OP_2_i - 1_P_2_j_ and OP_2_i__P_2_j - 1 have a single common point.

Calculate the number of good sets of pairs modulo 1000000007 (109 + 7).

平面上有一组点集 $S$。该点集不包含原点 $O(0,\,0)$，且对其中任意两个不同的点 $A$ 和 $B$，三角形 $OAB$ 的面积严格大于 0。

考虑一组点对：$(P_1,\,P_2),\,(P_3,\,P_4),\,\dots,\,(P_{2k-1},\,P_{2k})$。我们称该点对集合为“好”的，当且仅当满足以下条件：

• $k \geq 2$；
• 所有 $P_i$ 互不相同，且每个 $P_i$ 均属于 $S$；
• 对任意两对 $(P_{2i-1},\,P_{2i})$ 和 $(P_{2j-1},\,P_{2j})$（其中 $i \ne j$），三角形 $OP_{2i-1}P_{2j-1}$ 与 $OP_{2i}P_{2j}$ 的外接圆恰有一个公共点，且三角形 $OP_{2i-1}P_{2j}$ 与 $OP_{2i}P_{2j-1}$ 的外接圆也恰有一个公共点。

请计算“好”的点对集合的个数，结果对 $1000000007$（即 $10^9 + 7$）取模。

The first line contains a single integer n (1 ≤ n ≤ 1000) — the number of points in S. Each of the next n lines contains four integers a__i, b__i, c__i, d__i (0 ≤ |a__i|, |c__i| ≤ 50; 1 ≤ b__i, d__i ≤ 50; (a__i, c__i) ≠ (0, 0)). These integers represent a point .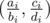

No two points coincide.

第一行包含一个整数 $n$（$1 \leq n \leq 1000$）——集合 $S$ 中点的个数。接下来的 $n$ 行每行包含四个整数 $a_i,\,b_i,\,c_i,\,d_i$（$0 \leq |a_i|,\,|c_i| \leq 50$；$1 \leq b_i,\,d_i \leq 50$；$(a_i,\,c_i) \neq (0,\,0)$）。这些整数表示一个点 。

任意两个点均不重合。

Print a single integer — the answer to the problem modulo 1000000007 (109 + 7).

输出一个整数——该问题答案对 $1000000007$（即 $10^9 + 7$）取模的结果。