CF391F3.Stock Trading

普及/提高-

通过率：0%

AC君温馨提醒

该题目为【codeforces】题库的题目，您提交的代码将被提交至codeforces进行远程评测，并由ACGO抓取测评结果后进行展示。由于远程测评的测评机由其他平台提供，我们无法保证该服务的稳定性，若提交后无反应，请等待一段时间后再进行重试。

题目描述

The first line contains two integers $n$ and $k$ , separated by a single space, with 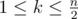. The $i$ -th of the following $n$ lines contains a single integer $p_{i}$ ( $0<=p_{i}<=10^{12}$ ), where $p_{i}$ represents the price at which someone can either buy or sell one share of stock on day $i$ .

The problem consists of three subproblems. The subproblems have different constraints on the input. You will get some score for the correct submission of the subproblem. The description of the subproblems follows.

In subproblem F1 (8 points), $n$ will be between $1$ and $3000$ , inclusive.
In subproblem F2 (15 points), $n$ will be between $1$ and $100000$ , inclusive.
In subproblem F3 (10 points), $n$ will be between $1$ and $4000000$ , inclusive.

输入格式

For this problem, the program will only report the amount of the optimal profit, rather than a list of trades that can achieve this profit.

Therefore, the program should print one line containing a single integer, the maximum profit Manao can achieve over the next $n$ days with the constraints of starting with no shares on the first day of trading, always owning either zero or one shares of stock, and buying at most $k$ shares over the course of the $n$ -day trading period.

输出格式

In the first example, the best trade overall is to buy at a price of $1$ on day 9 and sell at a price of $9$ on day 10 and the second best trade overall is to buy at a price of $2$ on day 1 and sell at a price of $9$ on day 4. Since these two trades do not overlap, both can be made and the profit is the sum of the profits of the two trades. Thus the trade strategy looks like this:

<pre class="verbatim"><br></br>2    | 7    | 3    | 9    | 8    | 7    | 9    | 7    | 1    | 9<br></br>buy  |      |      | sell |      |      |      |      | buy  | sell<br></br>

The total profit is then $(9-2)+(9-1)=15$ .

In the second example, even though Manao is allowed up to 5 trades there are only 4 profitable trades available. Making a fifth trade would cost Manao money so he only makes the following 4:

<pre class="verbatim"><br></br>2    | 7    | 3    | 9    | 8    | 7    | 9    | 7    | 1    | 9<br></br>buy  | sell | buy  | sell |      | buy  | sell |      | buy  | sell<br></br>

The total profit is then $(7-2)+(9-3)+(9-7)+(9-1)=21$ .

输入输出样例

输入#1
```
10 2
2
7
3
9
8
7
9
7
1
9
```
输出#1
```
15
```
输入#2
```
10 5
2
7
3
9
8
7
9
7
1
9
```
输出#2
```
21
```

说明/提示

<pre class="verbatim"><br></br>2    | 7    | 3    | 9    | 8    | 7    | 9    | 7    | 1    | 9<br></br>buy  |      |      | sell |      |      |      |      | buy  | sell<br></br>

The total profit is then $(9-2)+(9-1)=15$ .

In the second example, even though Manao is allowed up to 5 trades there are only 4 profitable trades available. Making a fifth trade would cost Manao money so he only makes the following 4:

<pre class="verbatim"><br></br>2    | 7    | 3    | 9    | 8    | 7    | 9    | 7    | 1    | 9<br></br>buy  | sell | buy  | sell |      | buy  | sell |      | buy  | sell<br></br>

The total profit is then $(7-2)+(9-3)+(9-7)+(9-1)=21$ .

首页