CF356D.Bags and Coins
普及/提高-
通过率:0%
AC君温馨提醒
该题目为【codeforces】题库的题目,您提交的代码将被提交至codeforces进行远程评测,并由ACGO抓取测评结果后进行展示。由于远程测评的测评机由其他平台提供,我们无法保证该服务的稳定性,若提交后无反应,请等待一段时间后再进行重试。
题目描述
When you were a child you must have been told a puzzle of bags and coins. Anyway, here's one of its versions:
A horse has three bags. The first bag has one coin, the second bag has one coin and the third bag has three coins. In total, the horse has three coins in the bags. How is that possible?
The answer is quite simple. The third bag contains a coin and two other bags.
This problem is a generalization of the childhood puzzle. You have n bags. You know that the first bag contains a1 coins, the second bag contains a2 coins, ..., the n -th bag contains an coins. In total, there are s coins. Find the way to arrange the bags and coins so that they match the described scenario or else state that it is impossible to do.
输入格式
The first line contains two integers n and s (1<=n,s<=70000) — the number of bags and the total number of coins. The next line contains n integers a1,a2,...,an (1<=ai<=70000) , where ai shows the number of coins in the i -th bag.
输出格式
If the answer doesn't exist, print -1.
Otherwise, print n lines, on the i -th line print the contents of the i -th bag. The first number in the line, ci (0<=ci<=ai) , must represent the number of coins lying directly in the i -th bag (the coins in the bags that are in the i -th bag are not taken into consideration). The second number in the line, ki (0<=k_{i}<n) must represent the number of bags that lie directly in the i -th bag (the bags that are inside the bags lying in the i -th bag are not taken into consideration). Next, the line must contain ki integers — the numbers of the bags that are lying directly in the i -th bag.
The total number of coins in the solution must equal s . If we count the total number of coins the i -th bag in the solution has, we should get ai .
No bag can directly lie in more than one bag. The bags can be nested in more than one level (see the second test case). If there are multiple correct answers, you can print any of them.
输入输出样例
输入#1
3 3 1 3 1
输出#1
1 0 1 2 3 1 1 0
输入#2
3 3 1 3 1
输出#2
1 0 2 1 3 0 1 1
输入#3
1 2 1
输出#3
-1
输入#4
8 10 2 7 3 4 1 3 1 2
输出#4
2 0 1 2 1 4 0 2 7 8 0 2 5 6 1 0 3 0 1 0 2 0
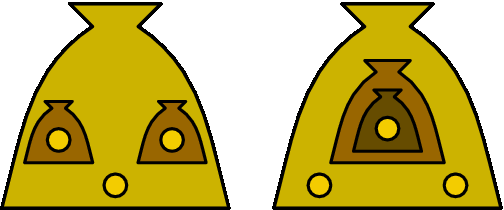
说明/提示
The pictures below show two possible ways to solve one test case from the statement. The left picture corresponds to the first test case, the right picture corresponds to the second one.