CF366E.Dima and Magic Guitar

Dima loves Inna very much. He decided to write a song for her. Dima has a magic guitar with n strings and m frets. Dima makes the guitar produce sounds like that: to play a note, he needs to hold one of the strings on one of the frets and then pull the string. When Dima pulls the i-th string holding it on the j-th fret the guitar produces a note, let's denote it as a__ij. We know that Dima's guitar can produce k distinct notes. It is possible that some notes can be produced in multiple ways. In other words, it is possible that a__ij = a__pq at (i, j) ≠ (p, q).

Dima has already written a song — a sequence of s notes. In order to play the song, you need to consecutively produce the notes from the song on the guitar. You can produce each note in any available way. Dima understood that there are many ways to play a song and he wants to play it so as to make the song look as complicated as possible (try to act like Cobein).

We'll represent a way to play a song as a sequence of pairs (x__i, y__i) (1 ≤ i ≤ s), such that the x__i-th string on the y__i-th fret produces the i-th note from the song. The complexity of moving between pairs (_x_1, _y_1) and (_x_2, _y_2) equals + 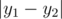. The complexity of a way to play a song is the maximum of complexities of moving between adjacent pairs.

Help Dima determine the maximum complexity of the way to play his song! The guy's gotta look cool!

迪马非常爱英娜。他决定为她写一首歌。迪马有一把神奇的吉他，共有 $n$ 根弦和 $m$ 品。迪马通过如下方式让吉他发声：要演奏一个音符，他需要按住某一根弦上的某一品，然后拨动该弦。当迪马按住第 $i$ 根弦的第 $j$ 品并拨动时，吉他发出一个音符，记作 $a_{ij}$。已知迪马的吉他总共能发出 $k$ 个不同的音符。某些音符可能有多种按法。换言之，可能存在 $(i,j) \neq (p,q)$，但满足 $a_{ij} = a_{pq}$。

迪马已经写好了一首歌——一个由 $s$ 个音符组成的序列。要演奏这首歌，需在吉他上依次奏出其中每个音符。每个音符均可采用任意一种可行的按法来演奏。迪马意识到，演奏这首歌的方式有很多，而他希望以尽可能“炫酷”的方式来演奏（努力模仿科贝因的风格）。

我们将一种演奏方式表示为一系列数对 $(x_i, y_i)$（其中 $1 \le i \le s$），使得在第 $x_i$ 根弦的第 $y_i$ 品处发声，恰好得到歌曲中的第 $i$ 个音符。从数对 $(x_1, y_1)$ 移动到 $(x_2, y_2)$ 的复杂度定义为
+ 。
一种演奏方式的复杂度定义为所有相邻数对之间移动复杂度的最大值。

请帮助迪马求出演奏这首歌所能达到的最大复杂度！这家伙必须看起来够酷！

The first line of the input contains four integers n, m, k and s (1 ≤ n, m ≤ 2000, 1 ≤ k ≤ 9, 2 ≤ s ≤ 105).

Then follow n lines, each containing m integers a__ij (1 ≤ a__ij ≤ k). The number in the i-th row and the j-th column (a__ij) means a note that the guitar produces on the i-th string and the j-th fret.

The last line of the input contains s integers q__i (1 ≤ q__i ≤ k) — the sequence of notes of the song.

输入的第一行包含四个整数 $n$、$m$、$k$ 和 $s$（$1 ≤ n, m ≤ 2000$，$1 ≤ k ≤ 9$，$2 ≤ s ≤ 10^5$）。

接下来是 $n$ 行，每行包含 $m$ 个整数 $a_{ij}$（$1 ≤ a_{ij} ≤ k$）。第 $i$ 行第 $j$ 列的数字 $a_{ij}$ 表示吉他第 $i$ 根弦、第 $j$ 品所发出的音符。

输入的最后一行包含 $s$ 个整数 $q_i$（$1 ≤ q_i ≤ k$）——即歌曲的音符序列。

In a single line print a single number — the maximum possible complexity of the song.

在一行中输出一个整数——歌曲可能达到的最大复杂度。