CF321E.Ciel and Gondolas

Fox Ciel is in the Amusement Park. And now she is in a queue in front of the Ferris wheel. There are n people (or foxes more precisely) in the queue: we use first people to refer one at the head of the queue, and n-th people to refer the last one in the queue.

There will be k gondolas, and the way we allocate gondolas looks like this:

• When the first gondolas come, the _q_1 people in head of the queue go into the gondolas.

• Then when the second gondolas come, the _q_2 people in head of the remain queue go into the gondolas.

  ...

• The remain q__k people go into the last (k-th) gondolas.

Note that _q_1, _q_2, ..., q__k must be positive. You can get from the statement that 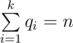and q__i > 0.

You know, people don't want to stay with strangers in the gondolas, so your task is to find an optimal allocation way (that is find an optimal sequence q) to make people happy. For every pair of people i and j, there exists a value u__ij denotes a level of unfamiliar. You can assume u__ij = u__ji for all i, j (1 ≤ i, j ≤ n) and u__ii = 0 for all i (1 ≤ i ≤ n). Then an unfamiliar value of a gondolas is the sum of the levels of unfamiliar between any pair of people that is into the gondolas.

A total unfamiliar value is the sum of unfamiliar values for all gondolas. Help Fox Ciel to find the minimal possible total unfamiliar value for some optimal allocation.

小狐 Ciel 来到了游乐园，此刻她正站在摩天轮前的队伍中。队伍中共有 $ n $ 个人（更准确地说，是 $ n $ 只狐狸）：我们称排在队伍最前端的人为第 1 人，排在队尾的人为第 $ n $ 人。

摩天轮共有 $ k $ 个座舱（gondolas），座舱的分配方式如下：

• 当第一个座舱到达时，队伍最前端的 $ q_1 $ 个人进入该座舱；
• 当第二个座舱到达时，剩余队伍最前端的 $ q_2 $ 个人进入该座舱；
  　　…
• 剩余的 $ q_k $ 个人进入最后一个（即第 $ k $ 个）座舱。

注意：$ q_1, q_2, \dots, q_k $ 必须均为正整数。由题意可知，，且对所有 $ i $，均有 $ q_i > 0 $。

众所周知，人们不愿与陌生人共乘一个座舱，因此你的任务是寻找一种最优的分配方案（即确定一个最优序列 $ q $），以使所有人尽可能满意。对于任意两个人 $ i $ 和 $ j $，给定一个值 $ u_{ij} $，表示他们之间的陌生程度。可假设对所有 $ i, j $（$ 1 \le i, j \le n $），均有 $ u_{ij} = u_{ji} $；且对所有 $ i $（$ 1 \le i \le n $），均有 $ u_{ii} = 0 $。那么，一个座舱的陌生值定义为：该座舱内所有人员两两之间的陌生程度之和。

总陌生值则为所有座舱陌生值之和。请帮助小狐 Ciel 找出某种最优分配下所能达到的最小总陌生值。

The first line contains two integers n and k (1 ≤ n ≤ 4000 and 1 ≤ k ≤ min(n, 800)) — the number of people in the queue and the number of gondolas. Each of the following n lines contains n integers — matrix u, (0 ≤ u__ij ≤ 9, u__ij = u__ji and u__ii = 0).

Please, use fast input methods (for example, please use BufferedReader instead of Scanner for Java).

第一行包含两个整数 $n$ 和 $k$（$1 \leq n \leq 4000$，$1 \leq k \leq \min(n, 800)$）—— 分别表示队列中的人数和缆车的数量。接下来的 $n$ 行每行包含 $n$ 个整数，构成矩阵 $u$（满足 $0 \leq u_{ij} \leq 9$，$u_{ij} = u_{ji}$ 且 $u_{ii} = 0$）。

请注意，使用快速输入方式（例如，在 Java 中请使用 BufferedReader 而非 Scanner）。

Print an integer — the minimal possible total unfamiliar value.

输出一个整数——最小可能的总不熟悉值。

In the first example, we can allocate people like this: {1, 2} goes into a gondolas, {3, 4, 5} goes into another gondolas.

In the second example, an optimal solution is : {1, 2, 3} | {4, 5, 6} | {7, 8}.

在第一个例子中，我们可以这样分配人员：{1, 2} 进入一艘缆车，{3, 4, 5} 进入另一艘缆车。

在第二个例子中，一个最优解是：{1, 2, 3} | {4, 5, 6} | {7, 8}。