CF331E1.Deja Vu

Everybody knows that we have been living in the Matrix for a long time. And in the new seventh Matrix the world is ruled by beavers.

So let's take beaver Neo. Neo has so-called "deja vu" outbursts when he gets visions of events in some places he's been at or is going to be at. Let's examine the phenomenon in more detail.

We can say that Neo's city is represented by a directed graph, consisting of $n$ shops and $m$ streets that connect the shops. No two streets connect the same pair of shops (besides, there can't be one street from A to B and one street from B to A). No street connects a shop with itself. As Neo passes some streets, he gets visions. No matter how many times he passes street $k$ , every time he will get the same visions in the same order. A vision is a sequence of shops.

We know that Neo is going to get really shocked if he passes the way from some shop $a$ to some shop $b$ , possible coinciding with $a$ , such that the list of visited shops in the real life and in the visions coincide.

Suggest beaver Neo such path of non-zero length. Or maybe you can even count the number of such paths modulo $1000000007$ $(10^{9}+7)$ ?..

The first line contains integers $n$ and $m$ — the number of shops and the number of streets, correspondingly, $1<=n<=50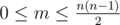$ , . Next $m$ lines contain the descriptions of the streets in the following format: $x_{i}$ $y_{i}$ $k_{i}$ $v_{1}$ $v_{2}$ ... $v_{k}$ , where $x_{i}$ and $y_{i}$ $(1<=x_{i},y_{i}<=n,x_{i}≠y_{i})$ are indices of shops connected by a street, $k_{i}$ $(0<=k_{i}<=n)$ is the number of visions on the way from $x_{i}$ to $y_{i}$ ; $v_{1}$ , $v_{2}$ , ..., $v_{k}$ $(1<=v_{i}<=n)$ describe the visions: the numbers of the shops Neo saw. Note that the order of the visions matters.

It is guaranteed that the total number of visions on all streets doesn't exceed $10^{5}$ .

• to get 50 points, you need to find any (not necessarily simple) path of length at most $2·n$ , that meets the attributes described above (subproblem E1);
• to get 50 more points, you need to count for each length from $1$ to $2·n$ the number of paths that have the attribute described above (subproblem E2).

Subproblem E1. In the first line print an integer $k$ $(1<=k<=2·n)$ — the numbers of shops on Neo's path. In the next line print $k$ integers — the number of shops in the order Neo passes them. If the graph doesn't have such paths or the length of the shortest path includes more than $2·n$ shops, print on a single line $0$ .

Subproblem E2. Print $2·n$ lines. The $i$ -th line must contain a single integer — the number of required paths of length $i$ modulo $1000000007$ $(10^{9}+7)$ .

The input in both samples are the same. The first sample contains the answer to the first subproblem, the second sample contains the answer to the second subproblem.