CF332D.Theft of Blueprints

Insurgents accidentally got hold of the plan of a top secret research polygon created on a distant planet for the needs of the Galaxy Empire. The insurgents suppose that this polygon is developing new deadly weapon. The polygon consists of n missile silos connected by bidirectional underground passages. The passages are linked to laboratories where research is conducted. Naturally, the passages are guarded severely: the passage between silos i and j is patrolled by c__i, j war droids.

The insurgents studied the polygon plan and noticed its unusual structure. As it turned out, for any k-element set of silos S there is exactly one silo that is directly connected by a passage with each silo from S (we'll call this silo adjacent with S). Having considered that, the insurgents decided to act as follows:

1. they choose a k-element set of silos S;
2. a group of scouts lands from the air into each silo from S;
3. each group moves along the corresponding passage to the silo, adjacent with S (as the scouts move, they check out the laboratories and watch for any signs of weapon blueprints);
4. in the silo, adjacent with S, the groups get on the ship and fly away.

The danger of the operation is the total number of droids that patrol the passages through which the scouts will go. The danger of the operation obviously only depends on the way to choose set S. The insurgents haven't yet decided on the exact silos to send the scouts to. However, they already want to start preparing the weapons for the scout groups. To do that, the insurgents need to know the mathematical average of the dangers of the operations that correspond to all possible ways to choose set S. Solve this problem to help the insurgents protect the ideals of the Republic!

叛军意外获取了一份绝密科研基地的规划图。该基地位于遥远的星球上，专为银河帝国的需要而建造。叛军推测，该基地正在研发一种新型致命武器。该基地由 $n$ 个导弹发射井组成，发射井之间通过双向地下通道相连。这些通道连接着开展研究的实验室。自然地，这些通道受到严密守卫：在发射井 $i$ 与 $j$ 之间的通道上，有 $c_{i,j}$ 个战争机器人进行巡逻。

叛军仔细研究了该基地的规划图，并注意到其结构极为特殊。事实证明，对于任意一个包含 $k$ 个发射井的集合 $S$，都恰好存在一个发射井，它通过通道直接连接到 $S$ 中的每一个发射井（我们将这个发射井称为集合 $S$ 的邻接发射井）。基于这一发现，叛军决定采取如下行动方案：

1. 他们选择一个大小为 $k$ 的发射井集合 $S$；
2. 一支侦察小队从空中空降至集合 $S$ 中的每一个发射井；
3. 每支小队沿对应的通道移动至集合 $S$ 的邻接发射井（在移动过程中，他们将勘察沿途的实验室，并搜寻任何武器设计图的迹象）；
4. 所有小队在邻接发射井处登上飞船撤离。

此次行动的危险程度，定义为所有侦察小队所经通道上巡逻的战争机器人总数。显然，该危险程度仅取决于集合 $S$ 的选取方式。叛军尚未最终确定具体向哪些发射井派遣侦察小队，但他们已亟需开始为侦察小队准备武器装备。为此，叛军需要知道：对所有可能的大小为 $k$ 的发射井集合 $S$，对应行动危险程度的数学期望值（即算术平均值）。请解决此问题，以协助叛军捍卫共和国的理想！

The first line contains two integers n and k (2 ≤ n ≤ 2000, 1 ≤ k ≤ n - 1) — the number of silos and the number of scout groups, correspondingly. The next n - 1 lines describe the polygon plan: the i-th of these lines contains n - i integers c__i, i + 1, c__i, i + 2, ..., c__i, n — the number of droids that patrol the corresponding passages (-1 ≤ c__i, j ≤ 109; if c__i, j =  -1, then silos i and j don't have a passage between them). All passages are bidirectional, that is, we can assume that c__i, j = c__j, i. No passages connect a silo with itself. It is guaranteed that the polygon plan meets the conditions of the problem statement.

第一行包含两个整数 $n$ 和 $k$（$2 \leq n \leq 2000$，$1 \leq k \leq n-1$），分别表示弹药库的数量和侦察小队的数量。接下来的 $n-1$ 行描述多边形布局：其中第 $i$ 行包含 $n-i$ 个整数 $c_{i,\,i+1},\,c_{i,\,i+2},\,\dots,\,c_{i,\,n}$，表示在对应通道中巡逻的机器人数量（$-1 \leq c_{i,\,j} \leq 10^9$；若 $c_{i,\,j} = -1$，则弹药库 $i$ 与 $j$ 之间没有通道）。所有通道均为双向的，即我们可以认为 $c_{i,\,j} = c_{j,\,i}$。不存在连接同一弹药库自身的通道。题目保证该多边形布局满足题面所给条件。

Print the average danger of the scouting operation, rounded down to an integer. Note that at the given limits the answer to the problem always fits into the standard integer 64-bit data type.

Please do not use the %lld specifier to write 64-bit integers in С++. It is preferred to use the cout stream or the %I64d specifier.

输出侦察行动的平均危险度，向下取整为整数。注意：在给定的数据限制下，本题的答案始终可用标准的 64 位整数类型表示。

在 C++ 中，请勿使用 %lld 格式说明符输出 64 位整数。推荐使用 cout 流或 %I64d 格式说明符。

In the first sample there are 6 one-element sets of silos. For sets {1}, {5} the operation danger will equal 8, for sets {3}, {6} — 3, for sets {2}, {4} — 5. The mathematical average equals .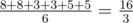

In the second sample there are 3 two-elements sets of silos: {1, 3} (danger equals 21), {1, 2} (danger equals 11), {2, 3} (danger equals 10). The average operation danger equals .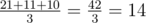

在第一个样例中，共有 6 个单元素粮仓集合。对于集合 {1}、{5}，危险度操作值为 8；对于集合 {3}、{6}，危险度操作值为 3；对于集合 {2}、{4}，危险度操作值为 5。数学平均值为 。

在第二个样例中，共有 3 个双元素粮仓集合：{1, 3}（危险度为 21）、{1, 2}（危险度为 11）、{2, 3}（危险度为 10）。平均危险度操作值为 。