CF303B.Rectangle Puzzle II

You are given a rectangle grid. That grid's size is n × m. Let's denote the coordinate system on the grid. So, each point on the grid will have coordinates — a pair of integers (x, y) (0 ≤ x ≤ n, 0 ≤ y ≤ m).

Your task is to find a maximum sub-rectangle on the grid (_x_1, _y_1, _x_2, _y_2) so that it contains the given point (x, y), and its length-width ratio is exactly (a, b). In other words the following conditions must hold: 0 ≤ _x_1 ≤ x ≤ _x_2 ≤ n, 0 ≤ _y_1 ≤ y ≤ _y_2 ≤ m, .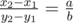

The sides of this sub-rectangle should be parallel to the axes. And values _x_1, _y_1, _x_2, _y_2 should be integers.

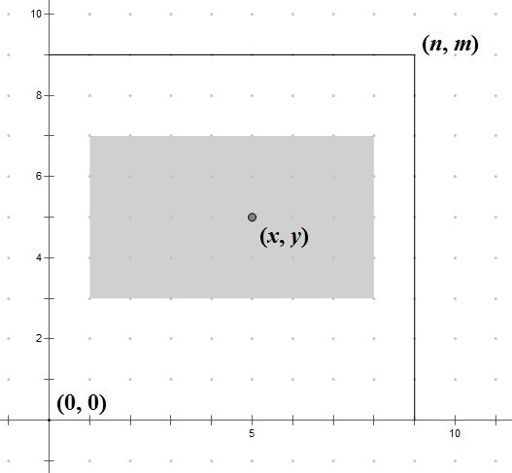If there are multiple solutions, find the rectangle which is closest to (x, y). Here "closest" means the Euclid distance between (x, y) and the center of the rectangle is as small as possible. If there are still multiple solutions, find the lexicographically minimum one. Here "lexicographically minimum" means that we should consider the sub-rectangle as sequence of integers (_x_1, _y_1, _x_2, _y_2), so we can choose the lexicographically minimum one.

给你一个矩形网格，其尺寸为 $n \times m$。我们在此网格上建立坐标系，因此网格上的每个点都有坐标——一对整数 $(x, y)$（其中 $0 \le x \le n$，$0 \le y \le m$）。

你的任务是在该网格中找出一个面积最大的子矩形 $(x_1, y_1, x_2, y_2)$，使得该子矩形包含给定点 $(x, y)$，且其长宽比恰好为 $(a, b)$。换言之，需满足以下条件：
$0 \le x_1 \le x \le x_2 \le n$，
$0 \le y_1 \le y \le y_2 \le m$，
。

该子矩形的边必须与坐标轴平行，且 $x_1, y_1, x_2, y_2$ 均为整数。

若存在多个解，则选择最接近$(x, y)$ 的矩形。“最接近”指 $(x, y)$ 到该矩形中心的欧几里得距离最小。若仍有多个解，则选择字典序最小的一个。“字典序最小”是指将子矩形视为整数序列 $(x_1, y_1, x_2, y_2)$，从中选出字典序最小者。

The first line contains six integers n, m, x, y, a, b (1 ≤ n, m ≤ 109, 0 ≤ x ≤ n, 0 ≤ y ≤ m, 1 ≤ a ≤ n, 1 ≤ b ≤ m).

第一行包含六个整数 $n$、$m$、$x$、$y$、$a$、$b$（$1 \le n, m \le 10^9$，$0 \le x \le n$，$0 \le y \le m$，$1 \le a \le n$，$1 \le b \le m$）。

Print four integers _x_1, _y_1, _x_2, _y_2, which represent the founded sub-rectangle whose left-bottom point is (_x_1, _y_1) and right-up point is (_x_2, _y_2).

输出四个整数 $x_1,\ y_1,\ x_2,\ y_2$，它们表示所找到的子矩形，其左下角点为 $(x_1,\ y_1)$，右上角点为 $(x_2,\ y_2)$。