CF303E.Random Ranking

Imagine a real contest or exam of n participants. Every participant will get a particular score. We can predict the standings board more or less, if we do some statistics on their previous performance.

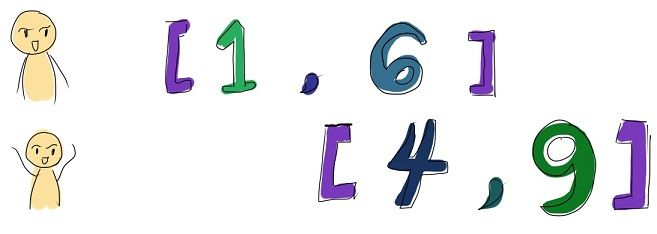Let's say the score of the participants will be uniformly distributed in interval [l__i, r__i] (the score can be a real number). Can you predict the standings board according to these data? In other words you should say for each participant the probability that he gets some fixed place in the scoreboard. The participants are sorted by increasing of their scores in the scoreboard. So, the participant with the largest score gets the last place.

想象一场有 $n$ 名参赛者的正式比赛或考试。每名参赛者将获得一个特定的分数。如果我们对其过往表现进行一些统计分析，便能在一定程度上预测最终的排名榜。

假设第 $i$ 名参赛者的得分在区间 $[l_i,\,r_i]$ 上服从均匀分布（得分可以是任意实数）。你能根据这些数据预测最终的排名榜吗？换言之，你需要对每名参赛者，计算其在最终排名榜中获得某一固定名次的概率。在排名榜中，参赛者按其得分升序排列；因此，得分最高的参赛者排在最后一名。

The first line contains integer n (1  ≤ n  ≤ 80), showing how many participants we have. Each of the next n lines contains our predictions, the i-th line contains a pair of integers l__i, r__i (0 ≤ l__i < r__i ≤ 109) as the distributed interval for participant i.

Consider the participants numbered from 1 to n in some way.

第一行包含一个整数 $n$（$1 \leq n \leq 80$），表示参赛者人数。接下来的 $n$ 行中，每行包含我们对一名参赛者的预测：第 $i$ 行包含一对整数 $l_i,\,r_i$（$0 \leq l_i < r_i \leq 10^9$），表示第 $i$ 名参赛者的得分分布区间。

假设参赛者被以某种方式编号为 $1$ 到 $n$。

Output a distributed matrix a of order n. The element a__ij of the matrix is the probability that participant i has rank j.

Your answer will considered correct if it has at most 10 - 6 absolute or relative error.

输出一个 $n$ 阶的分布式矩阵 $a$。矩阵中元素 $a_{ij}$ 表示参与者 $i$ 排名为 $j$ 的概率。

若你的答案的绝对误差或相对误差均不超过 $10^{-6}$，则视为正确。

The score probability distribution is continuous, which means, there is no possibility for a draw.

得分概率分布是连续的，这意味着不可能出现平局。