CF319A.Malek Dance Club

As a tradition, every year before IOI all the members of Natalia Fan Club are invited to Malek Dance Club to have a fun night together. Malek Dance Club has 2_n_ members and coincidentally Natalia Fan Club also has 2_n_ members. Each member of MDC is assigned a unique id i from 0 to 2_n_ - 1. The same holds for each member of NFC.

One of the parts of this tradition is one by one dance, where each member of MDC dances with a member of NFC. A dance pair is a pair of numbers (a, b) such that member a from MDC dances with member b from NFC.

The complexity of a pairs' assignment is the number of pairs of dancing pairs (a, b) and (c, d) such that a < c and b > d.

You are given a binary number of length n named x. We know that member i from MDC dances with member from NFC. Your task is to calculate the complexity of this assignment modulo 1000000007 (109 + 7).

Expression 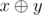denotes applying «XOR» to numbers x and y. This operation exists in all modern programming languages, for example, in C++ and Java it denotes as «^», in Pascal — «xor».

按照传统，每年 IOI 之前，娜塔莉亚粉丝俱乐部（NFC）的所有成员都会受邀前往马莱克舞蹈俱乐部（MDC）共度欢乐夜晚。马莱克舞蹈俱乐部有 $2^n$ 名成员，巧合的是，娜塔莉亚粉丝俱乐部也恰好有 $2^n$ 名成员。MDC 的每名成员被赋予一个唯一的编号 $i$，取值范围为 $0$ 到 $2^n - 1$；NFC 的每名成员同样被赋予一个唯一的编号，取值范围也为 $0$ 到 $2^n - 1$。

该传统活动的一个环节是“单人配对舞蹈”，即 MDC 的每名成员与 NFC 的一名成员配对共舞。一个舞蹈配对是一个数对 $(a,\,b)$，表示 MDC 编号为 $a$ 的成员与 NFC 编号为 $b$ 的成员共舞。

该配对方案的复杂度定义为满足如下条件的舞蹈配对对 $\big((a,\,b),\,(c,\,d)\big)$ 的数量：$a < c$ 且 $b > d$。

现给定一个长度为 $n$ 的二进制数 $x$。已知 MDC 中编号为 $i$ 的成员与 NFC 中编号为 的成员共舞。你的任务是计算该配对方案的复杂度，并对 $1000000007$（即 $10^9 + 7$）取模。

表达式 表示对数字 $x$ 和 $y$ 执行按位异或（XOR）运算。该运算在所有现代编程语言中均存在，例如在 C++ 和 Java 中用符号 ^ 表示，在 Pascal 中用 xor 表示。

The first line of input contains a binary number x of lenght n, (1 ≤ n ≤ 100).

This number may contain leading zeros.

输入的第一行包含一个长度为 $n$ 的二进制数 $x$（$1 ≤ n ≤ 100$）。

该数可能包含前导零。

Print the complexity of the given dance assignent modulo 1000000007 (109 + 7).

输出给定舞蹈分配的复杂度对 1000000007（$10^9 + 7$）取模的结果。