CF261D.Maxim and Increasing Subsequence

Maxim loves sequences, especially those that strictly increase. He is wondering, what is the length of the longest increasing subsequence of the given sequence a?

Sequence a is given as follows:

• the length of the sequence equals n × t;
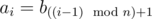• (1 ≤ i ≤ n × t), where operation 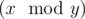means taking the remainder after dividing number x by number y.

Sequence _s_1,  _s_2,  ...,  s__r of length r is a subsequence of sequence _a_1,  _a_2,  ...,  a__n, if there is such increasing sequence of indexes _i_1, _i_2, ..., i__r (1  ≤  _i_1  <  _i_2  < ...   <  i__r  ≤  n), that a__i__j  =  s__j. In other words, the subsequence can be obtained from the sequence by crossing out some elements.

Sequence _s_1,  _s_2,  ...,  s__r is increasing, if the following inequality holds: _s_1 < _s_2 <  ... <  s__r.

Maxim have k variants of the sequence a. Help Maxim to determine for each sequence the length of the longest increasing subsequence.

马克西姆热爱序列，尤其是严格递增的序列。他想知道：给定序列 $a$ 的最长递增子序列（LIS）的长度是多少？

序列 $a$ 的定义如下：

• 序列的长度为 $n \times t$；
• $a_i = b_{(i-1) \bmod n + 1}$（其中 $1 \le i \le n \times t$），其中运算 $x \bmod y$ 表示 $x$ 除以 $y$ 后的余数。

长度为 $r$ 的序列 $s_1,\ s_2,\ \dots,\ s_r$ 是序列 $a_1,\ a_2,\ \dots,\ a_n$ 的一个子序列，当且仅当存在一个严格递增的下标序列 $i_1,\ i_2,\ \dots,\ i_r$（满足 $1 \le i_1 < i_2 < \dots < i_r \le n$），使得对所有 $j = 1, 2, \dots, r$ 都有 $a_{i_j} = s_j$。换言之，该子序列可通过从原序列中删去若干元素得到。

序列 $s_1,\ s_2,\ \dots,\ s_r$ 是递增的，当且仅当满足如下不等式：$s_1 < s_2 < \dots < s_r$。

马克西姆共有 $k$ 个不同的序列 $a$。请帮助他分别求出每个序列的最长递增子序列的长度。

The first line contains four integers k, n, maxb and t (1 ≤ k ≤ 10; 1 ≤ n, maxb ≤ 105; 1 ≤ t ≤ 109; n × maxb ≤ 2·107). Each of the next k lines contain n integers _b_1, _b_2, ..., b__n (1 ≤ b__i ≤ maxb).

Note that for each variant of the sequence a the values n, maxb and t coincide, the only arrays _b_s differ.

The numbers in the lines are separated by single spaces.

第一行包含四个整数 $k$、$n$、$\text{maxb}$ 和 $t$（$1 \leq k \leq 10$；$1 \leq n,\,\text{maxb} \leq 10^5$；$1 \leq t \leq 10^9$；$n \times \text{maxb} \leq 2\cdot10^7$）。接下来的 $k$ 行中，每行包含 $n$ 个整数 $b_1,\,b_2,\,...,\,b_n$（$1 \leq b_i \leq \text{maxb}$）。

注意：对于每个序列 $a$ 的变体，参数 $n$、$\text{maxb}$ 和 $t$ 均相同，仅数组 $b$ 不同。

各行中的数字以单个空格分隔。

Print k integers — the answers for the variants of the sequence a. Print the answers in the order the variants follow in the input.

输出 k 个整数——即序列 a 的各变体所对应的答案。请按照输入中各变体出现的顺序输出答案。