CF229C.Triangles

Alice and Bob don't play games anymore. Now they study properties of all sorts of graphs together. Alice invented the following task: she takes a complete undirected graph with n vertices, chooses some m edges and keeps them. Bob gets the 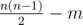remaining edges.

Alice and Bob are fond of "triangles" in graphs, that is, cycles of length 3. That's why they wonder: what total number of triangles is there in the two graphs formed by Alice and Bob's edges, correspondingly?

爱丽丝和鲍勃不再玩游戏了。现在他们一起研究各种图的性质。爱丽丝提出了如下问题：她取一个包含 $n$ 个顶点的完全无向图，从中选出 $m$ 条边保留下来。鲍勃则得到剩余的 条边。

爱丽丝和鲍勃都非常喜欢图中的“三角形”，即长度为 3 的环。因此，他们想知道：由爱丽丝和鲍勃各自所拥有的边构成的两个图中，三角形的总数分别是多少？

The first line contains two space-separated integers n and m (1 ≤ n ≤ 106, 0 ≤ m ≤ 106) — the number of vertices in the initial complete graph and the number of edges in Alice's graph, correspondingly. Then m lines follow: the i-th line contains two space-separated integers a__i, b__i (1 ≤ a__i, b__i ≤ n, a__i ≠ b__i), — the numbers of the two vertices connected by the i-th edge in Alice's graph. It is guaranteed that Alice's graph contains no multiple edges and self-loops. It is guaranteed that the initial complete graph also contains no multiple edges and self-loops.

Consider the graph vertices to be indexed in some way from 1 to n.

第一行包含两个以空格分隔的整数 $n$ 和 $m$（$1 \leq n \leq 10^6$，$0 \leq m \leq 10^6$），分别表示初始完全图的顶点数以及爱丽丝图中的边数。接下来是 $m$ 行：第 $i$ 行包含两个以空格分隔的整数 $a_i$、$b_i$（$1 \leq a_i, b_i \leq n$，$a_i \neq b_i$），表示爱丽丝图中第 $i$ 条边所连接的两个顶点的编号。保证爱丽丝图中不含重边和自环；也保证初始完全图中不含重边和自环。

设图的顶点以某种方式从 $1$ 到 $n$ 编号。

Print a single number — the total number of cycles of length 3 in Alice and Bob's graphs together.

Please, do not use the %lld specifier to read or write 64-bit integers in С++. It is advised to use the cin, cout streams or the %I64d specifier.

输出一个整数——Alice 和 Bob 的图中长度为 3 的环的总数。

请注意，在 C++ 中不要使用 %lld 说明符读取或写入 64 位整数。建议使用 cin、cout 流，或 %I64d 说明符。

In the first sample Alice has 2 triangles: (1, 2, 3) and (2, 3, 4). Bob's graph has only 1 triangle : (1, 4, 5). That's why the two graphs in total contain 3 triangles.

In the second sample Alice's graph has only one triangle: (1, 2, 3). Bob's graph has three triangles: (1, 4, 5), (2, 4, 5) and (3, 4, 5). In this case the answer to the problem is 4.

在第一个样例中，Alice 有 2 个三角形：$(1, 2, 3)$ 和 $(2, 3, 4)$；Bob 的图中仅有 1 个三角形：$(1, 4, 5)$。因此，这两张图总共包含 3 个三角形。

在第二个样例中，Alice 的图中仅有 1 个三角形：$(1, 2, 3)$；Bob 的图中有 3 个三角形：$(1, 4, 5)$、$(2, 4, 5)$ 和 $(3, 4, 5)$。此时该问题的答案为 4。