CF232C.Doe Graphs

John Doe decided that some mathematical object must be named after him. So he invented the Doe graphs. The Doe graphs are a family of undirected graphs, each of them is characterized by a single non-negative number — its order.

We'll denote a graph of order $k$ as $D(k)$ , and we'll denote the number of vertices in the graph $D(k)$ as $|D(k)|$ . Then let's define the Doe graphs as follows:

• $D(0)$ consists of a single vertex, that has number $1$ .
• $D(1)$ consists of two vertices with numbers $1$ and $2$ , connected by an edge.
• $D(n)$ for $n>=2$ is obtained from graphs $D(n-1)$ and $D(n-2)$ . $D(n-1)$ and $D(n-2)$ are joined in one graph, at that numbers of all vertices of graph $D(n-2)$ increase by $|D(n-1)|$ (for example, vertex number $1$ of graph $D(n-2)$ becomes vertex number $1+|D(n-1)|$ ). After that two edges are added to the graph: the first one goes between vertices with numbers $|D(n-1)|$ and $|D(n-1)|+1$ , the second one goes between vertices with numbers $|D(n-1)|+1$ and $1$ . Note that the definition of graph $D(n)$ implies, that $D(n)$ is a connected graph, its vertices are numbered from $1$ to $|D(n)|$ .

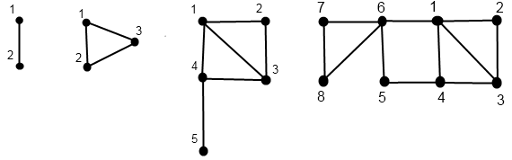The picture shows the Doe graphs of order 1, 2, 3 and 4, from left to right.John thinks that Doe graphs are that great because for them exists a polynomial algorithm for the search of Hamiltonian path. However, your task is to answer queries of finding the shortest-length path between the vertices $a_{i}$ and $b_{i}$ in the graph $D(n)$ .

A path between a pair of vertices $u$ and $v$ in the graph is a sequence of vertices $x_{1}$ , $x_{2}$ , $...$ , $x_{k}$ (k>1) such, that $x_{1}=u$ , $x_{k}=v$ , and for any $i$ (i<k) vertices $x_{i}$ and $x_{i+1}$ are connected by a graph edge. The length of path $x_{1}$ , $x_{2}$ , $...$ , $x_{k}$ is number $(k-1)$ .

The first line contains two integers $t$ and $n$ ( $1<=t<=10^{5}; 1<=n<=10^{3}$ ) — the number of queries and the order of the given graph. The $i$ -th of the next $t$ lines contains two integers $a_{i}$ and $b_{i}$ ( $1<=a_{i},b_{i}<=10^{16}$ , $a_{i}≠b_{i}$ ) — numbers of two vertices in the $i$ -th query. It is guaranteed that $a_{i},b_{i}<=|D(n)|$ .

Please, do not use the %lld specifier to read or write 64-bit integers in С++. It is preferred to use cin, cout streams or the %I64d specifier.

For each query print a single integer on a single line — the length of the shortest path between vertices $a_{i}$ and $b_{i}$ . Print the answers to the queries in the order, in which the queries are given in the input.