CF236B.Easy Number Challenge

普及/提高-

通过率：0%

AC君温馨提醒

该题目为【codeforces】题库的题目，您提交的代码将被提交至codeforces进行远程评测，并由ACGO抓取测评结果后进行展示。由于远程测评的测评机由其他平台提供，我们无法保证该服务的稳定性，若提交后无反应，请等待一段时间后再进行重试。

题目描述

Let's denote $d(n)$ as the number of divisors of a positive integer $n$ . You are given three integers $a$ , $b$ and $c$ . Your task is to calculate the following sum:

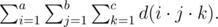Find the sum modulo $1073741824$ $(2^{30})$ .

输入格式

The first line contains three space-separated integers $a$ , $b$ and $c$ ( $1<=a,b,c<=100$ ).

输出格式

Print a single integer — the required sum modulo $1073741824$ $(2^{30})$ .

输入输出样例

输入#1
```
2 2 2
```
输出#1
```
20
```
输入#2
```
5 6 7
```
输出#2
```
1520
```

说明/提示

For the first example.

$d(1·1·1)=d(1)=1$ ;
$d(1·1·2)=d(2)=2$ ;
$d(1·2·1)=d(2)=2$ ;
$d(1·2·2)=d(4)=3$ ;
$d(2·1·1)=d(2)=2$ ;
$d(2·1·2)=d(4)=3$ ;
$d(2·2·1)=d(4)=3$ ;
$d(2·2·2)=d(8)=4$ .

So the result is $1+2+2+3+2+3+3+4=20$ .

首页