CF207A3.Beaver's Calculator 1.0

The Smart Beaver from ABBYY has once again surprised us! He has developed a new calculating device, which he called the "Beaver's Calculator $1.0$ ". It is very peculiar and it is planned to be used in a variety of scientific problems.

To test it, the Smart Beaver invited $n$ scientists, numbered from $1$ to $n$ . The $i$ -th scientist brought $k_{i}$ calculating problems for the device developed by the Smart Beaver from ABBYY. The problems of the $i$ -th scientist are numbered from $1$ to $k_{i}$ , and they must be calculated sequentially in the described order, since calculating each problem heavily depends on the results of calculating of the previous ones.

Each problem of each of the $n$ scientists is described by one integer $a_{i,j}$ , where $i$ ( $1<=i<=n$ ) is the number of the scientist, $j$ ( $1<=j<=k_{i}$ ) is the number of the problem, and $a_{i,j}$ is the number of resource units the calculating device needs to solve this problem.

The calculating device that is developed by the Smart Beaver is pretty unusual. It solves problems sequentially, one after another. After some problem is solved and before the next one is considered, the calculating device allocates or frees resources.

The most expensive operation for the calculating device is freeing resources, which works much slower than allocating them. It is therefore desirable that each next problem for the calculating device requires no less resources than the previous one.

You are given the information about the problems the scientists offered for the testing. You need to arrange these problems in such an order that the number of adjacent "bad" pairs of problems in this list is minimum possible. We will call two consecutive problems in this list a "bad pair" if the problem that is performed first requires more resources than the one that goes after it. Do not forget that the problems of the same scientist must be solved in a fixed order.

The first line contains integer $n$ — the number of scientists. To lessen the size of the input, each of the next $n$ lines contains five integers $k_{i}$ , $a_{i,1}$ , $x_{i}$ , $y_{i}$ , $m_{i}$ ( $0<=a_{i,1}<m_{i}<=10^{9}$ , $1<=x_{i},y_{i}<=10^{9}$ ) — the number of problems of the $i$ -th scientist, the resources the first problem requires and three parameters that generate the subsequent values of $a_{i,j}$ . For all $j$ from $2$ to $k_{i}$ , inclusive, you should calculate value $a_{i,j}$ by formula $a_{i,j}=(a_{i,j-1}*x_{i}+y_{i})$ $mod$ $m_{i}$ , where $a$ $mod$ $b$ is the operation of taking the remainder of division of number $a$ by number $b$ .

To get the full points for the first group of tests it is sufficient to solve the problem with $n=2$ , $1<=k_{i}<=2000$ .

To get the full points for the second group of tests it is sufficient to solve the problem with $n=2$ , $1<=k_{i}<=200000$ .

To get the full points for the third group of tests it is sufficient to solve the problem with $1<=n<=5000$ , $1<=k_{i}<=5000$ .

On the first line print a single number — the number of "bad" pairs in the optimal order.

If the total number of problems does not exceed $200000$ , also print 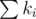lines — the optimal order of the problems. On each of these lines print two integers separated by a single space — the required number of resources for the problem and the number of the scientist who offered this problem, respectively. The scientists are numbered from $1$ to $n$ in the order of input.

In the first sample $n=2$ , $k_{1}=2$ , $a_{1,1}=1$ , $a_{1,2}=2$ , $k_{2}=2$ , $a_{2,1}=3$ , $a_{2,2}=4$ . We've got two scientists, each of them has two calculating problems. The problems of the first scientist require $1$ and $2$ resource units, the problems of the second one require $3$ and $4$ resource units. Let's list all possible variants of the calculating order (each problem is characterized only by the number of resource units it requires): $(1,2,3,4)$ , $(1,3,2,4)$ , $(3,1,2,4)$ , $(1,3,4,2)$ , $(3,4,1,2)$ , $(3,1,4,2)$ .

Sequence of problems $(1,3,2,4)$ has one "bad" pair ( $3$ and $2$ ), $(3,1,4,2)$ has two "bad" pairs ( $3$ and $1$ , $4$ and $2$ ), and $(1,2,3,4)$ has no "bad" pairs.