CF216D.Spider's Web

Paw the Spider is making a web. Web-making is a real art, Paw has been learning to do it his whole life. Let's consider the structure of the web.

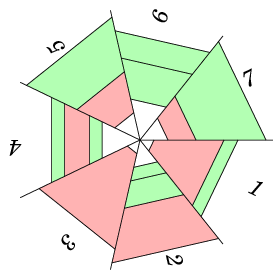There are n main threads going from the center of the web. All main threads are located in one plane and divide it into n equal infinite sectors. The sectors are indexed from 1 to n in the clockwise direction. Sectors i and i + 1 are adjacent for every i, 1 ≤ i < n. In addition, sectors 1 and n are also adjacent.

Some sectors have bridge threads. Each bridge connects the two main threads that make up this sector. The points at which the bridge is attached to the main threads will be called attachment points. Both attachment points of a bridge are at the same distance from the center of the web. At each attachment point exactly one bridge is attached. The bridges are adjacent if they are in the same sector, and there are no other bridges between them.

A cell of the web is a trapezoid, which is located in one of the sectors and is bounded by two main threads and two adjacent bridges. You can see that the sides of the cell may have the attachment points of bridges from adjacent sectors. If the number of attachment points on one side of the cell is not equal to the number of attachment points on the other side, it creates an imbalance of pulling forces on this cell and this may eventually destroy the entire web. We'll call such a cell unstable. The perfect web does not contain unstable cells.

Unstable cells are marked red in the figure. Stable cells are marked green.

Paw the Spider isn't a skillful webmaker yet, he is only learning to make perfect webs. Help Paw to determine the number of unstable cells in the web he has just spun.

蜘蛛帕乌正在织网。织网是一门真正的艺术，帕乌毕生都在学习这门技艺。我们来考察一下这张网的结构。

从网的中心出发，共有 $n$ 条主丝线。所有主丝线均位于同一平面内，并将该平面划分为 $n$ 个相等的无限扇形区域。这些扇形区域按顺时针方向编号为 $1$ 至 $n$。对每个满足 $1 \le i < n$ 的 $i$，扇形 $i$ 与扇形 $i+1$ 相邻；此外，扇形 $1$ 与扇形 $n$ 也相邻。

某些扇形区域内存在桥丝线。每条桥丝线连接构成该扇形的两条主丝线。桥丝线在主丝线上附着的点称为附着点。一条桥丝线的两个附着点到网中心的距离相等。每个附着点上恰好附着一条桥丝线。若两条桥丝线位于同一扇形内，且其间不存在其他桥丝线，则称这两条桥丝线相邻。

网的一个“单元”是一个梯形区域，它位于某个扇形内，且由两条主丝线及两条相邻的桥丝线围成。可以看出，该单元的边可能带有来自相邻扇形的桥丝线的附着点。若单元某一边上的附着点数量不等于另一边上的附着点数量，则该单元将受到不平衡的拉力作用，最终可能导致整张网被破坏。我们将此类单元称为不稳定单元。一张完美的网中不包含任何不稳定单元。

图中用红色标出了不稳定单元，绿色标出了稳定单元。

蜘蛛帕乌尚非一位娴熟的织网者，他目前仅在学习如何织出完美的网。请帮助帕乌确定他刚刚织就的这张网中不稳定单元的数量。

The first line contains integer n (3 ≤ n ≤ 1000) — the number of main threads.

The i-th of following n lines describe the bridges located in the i-th sector: first it contains integer k__i (1 ≤ k__i ≤ 105) equal to the number of bridges in the given sector. Then follow k__i different integers p__ij (1 ≤ p__ij ≤ 105; 1 ≤ j ≤ k__i). Number p__ij equals the distance from the attachment points of the j-th bridge of the i-th sector to the center of the web.

It is guaranteed that any two bridges between adjacent sectors are attached at a different distance from the center of the web. It is guaranteed that the total number of the bridges doesn't exceed 105.

第一行包含一个整数 $n$（$3 \leq n \leq 1000$）—— 主线程的数量。

接下来的 $n$ 行中，第 $i$ 行描述第 $i$ 个扇区中的蛛桥：首先是一个整数 $k_i$（$1 \leq k_i \leq 10^5$），表示该扇区中蛛桥的数量；随后是 $k_i$ 个互不相同的整数 $p_{ij}$（$1 \leq p_{ij} \leq 10^5$；$1 \leq j \leq k_i$）。数值 $p_{ij}$ 表示第 $i$ 个扇区中第 $j$ 座蛛桥的固定点到蛛网中心的距离。

保证任意两座相邻扇区之间的蛛桥，其固定点到蛛网中心的距离均不相同。保证蛛桥的总数不超过 $10^5$。

Print a single integer — the number of unstable cells in Paw the Spider's web.

输出一个整数——Paw 蜘蛛的蛛网中不稳定单元格的数量。