CF156E.Mrs. Hudson's Pancakes

Mrs. Hudson hasn't made her famous pancakes for quite a while and finally she decided to make them again. She has learned $m$ new recipes recently and she can't wait to try them. Those recipes are based on $n$ special spices. Mrs. Hudson has these spices in the kitchen lying in jars numbered with integers from $0$ to $n-1$ (each spice lies in an individual jar). Each jar also has the price of the corresponding spice inscribed — some integer $a_{i}$ .

We know three values for the $i$ -th pancake recipe: $d_{i}$ , $s_{i}$ , $c_{i}$ . Here $d_{i}$ and $c_{i}$ are integers, and $s_{i}$ is the pattern of some integer written in the numeral system with radix $d_{i}$ . The pattern contains digits, Latin letters (to denote digits larger than nine) and question marks. Number $x$ in the $d_{i}$ -base numeral system matches the pattern $s_{i}$ , if we can replace question marks in the pattern with digits and letters so that we obtain number $x$ (leading zeroes aren't taken into consideration when performing the comparison). More formally: each question mark should be replaced by exactly one digit or exactly one letter. If after we replace all question marks we get a number with leading zeroes, we can delete these zeroes. For example, number 40A9875 in the $11$ -base numeral system matches the pattern "??4??987?", and number 4A9875 does not.

To make the pancakes by the $i$ -th recipe, Mrs. Hudson should take all jars with numbers whose representation in the $d_{i}$ -base numeral system matches the pattern $s_{i}$ . The control number of the recipe ( $z_{i}$ ) is defined as the sum of number $c_{i}$ and the product of prices of all taken jars. More formally: 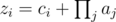(where $j$ is all such numbers whose representation in the $d_{i}$ -base numeral system matches the pattern $s_{i}$ ).

Mrs. Hudson isn't as interested in the control numbers as she is in their minimum prime divisors. Your task is: for each recipe $i$ find the minimum prime divisor of number $z_{i}$ . If this divisor exceeds $100$ , then you do not have to find it, print -1.

The first line contains the single integer $n$ ( $1<=n<=10^{4}$ ). The second line contains space-separated prices of the spices $a_{0},a_{1},...,a_{n-1}$ , where $a_{i}$ is an integer ( $1<=a_{i}<=10^{18}$ ).

The third line contains the single integer $m$ ( $1<=m<=3·10^{4}$ ) — the number of recipes Mrs. Hudson has learned.

Next $m$ lines describe the recipes, one per line. First you are given an integer $d_{i}$ , written in the decimal numeral system ( $2<=d_{i}<=16$ ). Then after a space follows the $s_{i}$ pattern — a string from $1$ to $30$ in length, inclusive, consisting of digits from "0" to "9", letters from "A" to "F" and signs "?". Letters from "A" to "F" should be considered as digits from $10$ to $15$ correspondingly. It is guaranteed that all digits of the pattern (including the digits that are represented by letters) are strictly less than $d_{i}$ . Then after a space follows an integer $c_{i}$ , written in the decimal numeral system ( $1<=c_{i}<=10^{18}$ ).

Please do not use the %lld specificator to read or write 64-bit integers in С++, in is preferred to use cin, cout, strings or the %I64d specificator instead.

For each recipe count by what minimum prime number the control number is divided and print this prime number on the single line. If this number turns out larger than $100$ , print -1.

In the first test any one-digit number in the binary system matches. The jar is only one and its price is equal to $1$ , the number $c$ is also equal to $1$ , the control number equals $2$ . The minimal prime divisor of $2$ is $2$ .

In the second test there are $4$ jars with numbers from $0$ to $3$ , and the prices are equal $2$ , $3$ , $5$ and $7$ correspondingly — the first four prime numbers. In all recipes numbers should be two-digit. In the first recipe the second digit always is $0$ , in the second recipe the second digit always is $1$ , in the third recipe the first digit must be $0$ , in the fourth recipe the first digit always is $1$ . Consequently, the control numbers ​​are as follows: in the first recipe $2×5+11=21$ (the minimum prime divisor is $3$ ), in the second recipe $3×7+13=44$ (the minimum prime divisor is $2$ ), in the third recipe $2×3+17=23$ (the minimum prime divisor is $23$ ) and, finally, in the fourth recipe $5×7+19=54$ (the minimum prime divisor is $2$ ).

In the third test, the number should consist of fourteen digits and be recorded in a sixteen-base numeral system. Number $0$ (the number of the single bottles) matches, the control number will be equal to $10^{18}+1$ . The minimum prime divisor of this number is equal to $101$ and you should print -1.