CF123E.Maze

A maze is represented by a tree (an undirected graph, where exactly one way exists between each pair of vertices). In the maze the entrance vertex and the exit vertex are chosen with some probability. The exit from the maze is sought by Deep First Search. If there are several possible ways to move, the move is chosen equiprobably. Consider the following pseudo-code:

DFS(x)
if x == exit vertex then
finish search
flag[x] <- TRUE
random shuffle the vertices' order in V(x) // here all permutations have equal probability to be chosen
for i <- 1 to length[V] do
if flag[V[i]] = FALSE then
count++;
DFS(y);
count++;

V(x) is the list vertices adjacent to x. The flag array is initially filled as FALSE. DFS initially starts with a parameter of an entrance vertex. When the search is finished, variable count will contain the number of moves.

Your task is to count the mathematical expectation of the number of moves one has to do to exit the maze.

迷宫由一棵树（即一个无向图，其中任意两个顶点之间恰好存在唯一一条路径）表示。在该迷宫中，入口顶点与出口顶点以某种概率被选定。迷宫的出口通过深度优先搜索（DFS）来寻找；当存在多个可选移动方向时，各方向被等概率地选择。考虑如下伪代码：

DFS(x)
if x == 出口顶点 then
结束搜索
flag[x] <- TRUE
对 V(x) 中的顶点顺序进行随机打乱 // 此处所有排列被选中的概率均相等
for i <- 1 to length[V] do
if flag[V[i]] == FALSE then
count++;
DFS(V[i]);
count++;

V(x) 表示与顶点 x 相邻的所有顶点构成的列表。数组 flag 初始时全部设为 FALSE。DFS 从入口顶点作为参数开始执行。当搜索结束时，变量 count 的值即为所执行的移动次数。

你的任务是计算成功走出迷宫所需移动次数的数学期望值。

The first line determines the number of vertices in the graph n (1 ≤ n ≤ 105). The next n - 1 lines contain pairs of integers a__i and b__i, which show the existence of an edge between a__i and b__i vertices (1 ≤ a__i, b__i ≤ n). It is guaranteed that the given graph is a tree.

Next n lines contain pairs of non-negative numbers x__i and y__i, which represent the probability of choosing the i-th vertex as an entrance and exit correspondingly. The probabilities to choose vertex i as an entrance and an exit equal 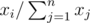and 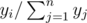correspondingly. The sum of all x__i and the sum of all y__i are positive and do not exceed 106.

第一行确定图中顶点的数量 $n$（$1 ≤ n ≤ 10^5$）。接下来的 $n - 1$ 行每行包含一对整数 $a_i$ 和 $b_i$，表示顶点 $a_i$ 与 $b_i$ 之间存在一条边（$1 ≤ a_i,\,b_i ≤ n$）。保证所给图是一棵树。

接下来的 $n$ 行每行包含一对非负数 $x_i$ 和 $y_i$，分别表示选择第 $i$ 个顶点作为入口和出口的概率。选择顶点 $i$ 作为入口和出口的概率分别为 和 。所有 $x_i$ 的总和以及所有 $y_i$ 的总和均为正数，且均不超过 $10^6$。

Print the expectation of the number of moves. The absolute or relative error should not exceed 10 - 9.

输出移动次数的期望值。绝对或相对误差不得超过 $10^{-9}$。

In the first sample the entrance vertex is always 1 and the exit vertex is always 2.

In the second sample the entrance vertex is always 1 and the exit vertex with the probability of 2/5 will be 2 of with the probability if 3/5 will be 3. The mathematical expectations for the exit vertices 2 and 3 will be equal (symmetrical cases). During the first move one can go to the exit vertex with the probability of 0.5 or to go to a vertex that's not the exit vertex with the probability of 0.5. In the first case the number of moves equals 1, in the second one it equals 3. The total mathematical expectation is counted as 2 / 5 × (1 × 0.5 + 3 × 0.5) + 3 / 5 × (1 × 0.5 + 3 × 0.5)

在第一个样例中，入口顶点始终为 1，出口顶点始终为 2。

在第二个样例中，入口顶点始终为 1，出口顶点以 $2/5$ 的概率为 2，以 $3/5$ 的概率为 3。出口顶点 2 和 3 的数学期望相等（对称情形）。在第一步中，以 $0.5$ 的概率直接到达出口顶点，或以 $0.5$ 的概率到达一个非出口顶点。在前一种情况下，移动步数为 1；在后一种情况下，移动步数为 3。总的数学期望为

$$2\,/\,5\,\times\,(1\,\times\,0.5\,+\,3\,\times\,0.5)\,+\,3\,/\,5\,\times\,(1\,\times\,0.5\,+\,3\,\times\,0.5)$$