CF97C.Winning Strategy

One university has just found out about a sport programming contest called ACM ICPC v2.0. This contest doesn't differ much from the well-known ACM ICPC, for example, the participants are not allowed to take part in the finals more than two times. However, there is one notable difference: the teams in the contest should consist of exactly n participants.

Having taken part in several ACM ICPC v2.0 finals and having not won any medals, the students and the university governors realized that it's high time they changed something about the preparation process. Specifically, as the first innovation it was decided to change the teams' formation process. Having spent considerable amount of time on studying the statistics of other universities' performance, they managed to receive some interesting information: the dependence between the probability of winning a medal and the number of team members that participated in the finals in the past. More formally, we know n + 1 real numbers _p_0 ≤ _p_1 ≤ ... ≤ p__n, where p__i is the probability of getting a medal on the finals if the team has i participants of previous finals, and other n - i participants arrived to the finals for the first time.

Despite such useful data, the university governors are unable to determine such team forming tactics that would provide the maximum probability of winning a medal at ACM ICPC v2.0 finals on average (we are supposed to want to provide such result to the far future and we are also supposed to have an endless supply of students). And how about you, can you offer such optimal tactic? At the first stage the university governors want to know the value of maximum average probability.

More formally, suppose that the university sends a team to the k-th world finals. The team has a__k participants of previous finals (0 ≤ a__k ≤ n). Since each person can participate in the finals no more than twice, the following condition must be true: 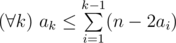. Your task is to choose sequence 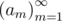so that the limit Ψ exists and it's value is maximal:

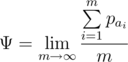As 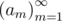is an infinite sequence, you should only print the maximum value of the Ψ limit.

某所大学刚刚了解到一项名为 ACM ICPC v2.0 的程序设计竞赛。该竞赛与广为人知的 ACM ICPC 并无太大差异——例如，参赛者最多只能参加两次决赛。但存在一个显著区别：每支参赛队必须恰好由 n 名队员组成。

在多次参加 ACM ICPC v2.0 决赛却未能获得任何奖牌后，该校学生与校方管理层意识到，是时候对备赛流程进行改革了。具体而言，作为首项创新举措，他们决定改革组队机制。经过大量时间研究其他高校的参赛表现统计数据，他们获得了一项有趣的信息：获奖牌概率与队内曾参加过以往决赛的队员人数之间存在依赖关系。更准确地说，我们已知 n + 1 个实数 _p_₀ ≤ _p_₁ ≤ … ≤ p__n，其中 p__i 表示：若一支队伍中有 i 名队员曾参加过以往的决赛，其余 n − i 名队员则是首次参赛，则该队在决赛中获得奖牌的概率。

尽管掌握了如此有价值的数据，该校管理层仍无法确定一种最优的组队策略，以使得该校在 ACM ICPC v2.0 决赛中平均获奖牌概率最大化（我们假定目标是为遥远的未来持续取得优异成绩，且学校拥有无限供给的学生资源）。那么，你能否提出这样一种最优策略？目前，校方管理层希望首先知道该最大平均概率的数值。

更形式化地，设该校派队参加第 k 届世界决赛，该队中有 a__k 名队员曾参加过以往决赛（0 ≤ a__k ≤ n）。由于每人至多可参加两次决赛，以下约束必须成立：

你的任务是选择序列

使得极限 Ψ 存在，并使其取值最大：

由于

是一个无穷序列，你只需输出该极限 Ψ 的最大可能值。

The first line contains an integer n (3 ≤ n ≤ 100), n is the number of team participants. The second line contains n + 1 real numbers with no more than 6 digits after decimal point p__i (0 ≤ i ≤ n, 0 ≤ p__i ≤ 1) — the probability of that the team will win a medal if it contains i participants who has already been on the finals. Also the condition p__i ≤ p__i + 1 should be fulfilled for all 0 ≤ i ≤ n - 1.

第一行包含一个整数 $n$（$3 \leq n \leq 100$），$n$ 表示队伍的参赛人数。
第二行包含 $n+1$ 个实数 $p_i$（$0 \leq i \leq n$，$0 \leq p_i \leq 1$），每个实数最多保留小数点后 6 位数字——表示当队伍中已有 $i$ 名成员曾参加过决赛时，该队伍获得奖牌的概率。
此外，对所有 $0 \leq i \leq n-1$，需满足条件 $p_i \leq p_{i+1}$。

Print the only real number — the expected average number of medals won per year if the optimal strategy is used. The result may have absolute or relative error 10 - 6.

输出唯一的实数——在采用最优策略的情况下，每年平均获得奖牌数的期望值。结果的绝对或相对误差不得超过 $10^{-6}$。

In the second test, no matter what participants the team contains, it is doomed to be successful.

在第二次测试中，无论队伍包含哪些参与者，它注定会成功。