CF113D.Museum

One day as Petya and his friend Vasya were having one of their numerous trips, they decided to visit a museum castle. The museum has a specific shape: it consists of $n$ rooms connected with $m$ corridors so that one can access any room from any other one.

After the two friends had a little walk around the museum, they decided to split and watch the pieces of art each of them found interesting. They agreed to meet in one of the rooms at six p.m. However, they forgot one quite essential thing: they didn't specify the place to meet and when the time came, they started to rush about the museum looking for each other (they couldn't call each other as roaming made a call's cost skyrocket).

Yet, even despite the whole rush, they couldn't get enough of the pieces of art, that's why each of them has the following strategy: each minute he make a decision where to go — with probability $p_{i}$ he doesn't move to any other place during this minute (i.e. he stays in the room). With probability $1-p_{i}$ he equiprobably choose one of the adjacent rooms and went there along the corridor. Here $i$ is the ordinal number of the current room. Building was expensive in ancient times, that's why each corridor connected two different rooms, and any two rooms had no more than one corridor between them.

The boys act simultaneously. As the corridors are dark, it is impossible to meet there; however, one can walk along the corridors in both directions (besides, the two boys can be going through the same corridor simultaneously without meeting). The boys act like that until they meet each other. More formally, the two friends meet when at some moment of time both of them decided to appear in the same room.

For each room find the probability that the boys will meet there considering that at 6 p.m. they are positioned in rooms $a$ and $b$ correspondingly.

The first line contains four integers: $n$ $(1<=n<=22)$ , representing the numbers of rooms; $m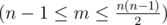$ , representing the number of corridors; $a,b$ $(1<=a,b<=n)$ , representing the numbers of Petya's and Vasya's starting rooms correspondingly.

Next $m$ lines contain pairs of numbers — the numbers of rooms connected by a corridor. Next $n$ lines contain probabilities $p_{i}$ $(0.01<=p_{i}<=0.99)$ with the accuracy of up to four digits after the decimal point — the probability to stay in room $i$ .

It is guaranteed that every room can be reached from every other room by corridors.

In the only line print $n$ space-separated numbers, the $i$ -th number should represent the probability that the friends meet in the $i$ -th room with absolute or relative error of no more than $10^{-6}$ .

In the first sample the museum is symmetric. That means the probabilities to meet in rooms 1 and 2 are equal. And their sum equals to one. So, each probability equals $0.5$ .